
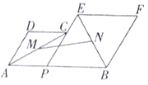
【题目】如图,AB=4,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段AB上移动时,点M,N之间的距离最短为( ).
A.![]() B.
B.![]() C.2D.3
C.2D.3
【答案】A
【解析】
连接PM、PN.首先证明∠MPN=90°,设PA=2a,则PB=4-2a,PM=a,PN=![]() (2a),MN2关于a的二次函数,利用二次函数的性质即可解决问题.
(2a),MN2关于a的二次函数,利用二次函数的性质即可解决问题.
连接PM、PN.
∵四边形APCD和四边形PBFE是菱形,∠DAP=60°,
∴∠APC=120°,∠EPB=60°,
∵M,N分别是对角线AC,BE的中点,
∴∠CPM=![]() ∠APC=60°,∠EPN=
∠APC=60°,∠EPN=![]() ∠EPB=30°,PM⊥AC,PN⊥BE,
∠EPB=30°,PM⊥AC,PN⊥BE,
∴∠MPN=60°+30°=90°,
∵∠CAP=![]() ∠DAP=30°,∠PBN=
∠DAP=30°,∠PBN=![]() ∠PBE=30°,
∠PBE=30°,
∴设PA=2a,则PB=42a,PM=a,PN=![]() (2a),
(2a),
∴MN2=![]() =
=![]() =
=![]() ,
,
∴当a=![]() 时,点M,N之间的距离最短,最短距离为
时,点M,N之间的距离最短,最短距离为![]() .
.
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
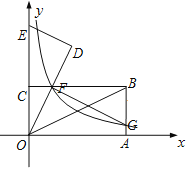
【题目】在如图平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA、OC分别落在x轴和y轴上,OB是矩形的对角线.将△OAB绕点O逆时针旋转,使点B落在y轴上,得到△ODE,OD与CB相交于点F,反比例函数y=![]() (x>0)的图象经过点F,交AB于点G.
(x>0)的图象经过点F,交AB于点G.
(1)求k的值和点G的坐标;
(2)连接FG,则图中是否存在与△BFG相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;
(3)在线段OA上存在这样的点P,使得△PFG是等腰三角形.请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BCD=90°,且BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)当α=125°时,∠ABC= °;
(2)求证:AC=CE;
(3)若△ABC的外心在其内部,直接写出α的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红灯笼,象征着阖家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
(1)求甲、乙两种灯笼每对的进价;
(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对:物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.
①求出y与x之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:![]() ,记为
,记为![]() ,它与
,它与![]() 轴交于点
轴交于点![]() ,
,![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ;…,如此进行下去,直至得
;…,如此进行下去,直至得![]() .
.
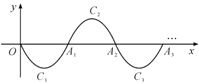
(1)请写出抛物线![]() 的解析式:________;
的解析式:________;
(2)若![]() 在第10段抛物线
在第10段抛物线![]() 上,则
上,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
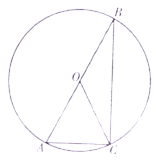
【题目】如图,⊙O为Rt△ABC的外接圆,弦AC的弦心距为5.
(1)尺规作图:作出∠BOC的平分线,并标出它与劣弧BC的交点E.(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
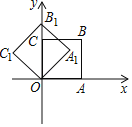
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE、CD 相交于点 A,连接 BC,DE,下列条件中不能判断△ABC∽ADE 的是( )
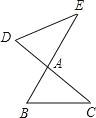
A. ∠B=∠D B. ∠C=∠E C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com