
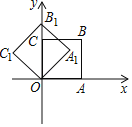
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
【答案】D
【解析】根据图形可知:点B在以O为圆心,以OB为半径的圆上运动,由旋转可知:将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,可得对应点B的坐标,根据规律发现是8次一循环,可得结论.
∵四边形OABC是正方形,且OA=1,
∴B(1,1),
连接OB,
由勾股定理得:OB=![]() ,
,
由旋转得:OB=OB1=OB2=OB3=…=![]() ,
,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,
∴B1(0,![]() ),B2(-1,1),B3(-
),B2(-1,1),B3(-![]() ,0),…,
,0),…,
发现是8次一循环,所以2018÷8=252…余2,
∴点B2018的坐标为(-1,1)
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m).
参考值:sin37°=0.60,cos37°=0.80,tan37°=0.75.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读短文,然后回答短文后面所给出的问题:对于三个数a,b,c的平均数,最小的数都可以符号来表示,我们规定M{a,b,c}表示这三个数的平均数,min{a,b,c}表示这三个数中最小的数,max{a,b,c}表示这三个数中最大的数.例如:M{1,2,3}=![]() ,min{1,2,3}=1,max{1,2,3}=3,M{1,2,a}=
,min{1,2,3}=1,max{1,2,3}=3,M{1,2,a}=![]() =
=![]() .
.
(1)请填空:min{1,3,2}=___________.若x<0,则max{2,(x+1)2+2,x+1}=__________.
(2)若M{2x24x5,72,x2+10x7}=max{10,2x2+4x+12,8},求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
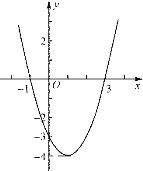
(1)写出方程ax2+bx+c=0(a≠0)的实数解;
(2)若方程ax2+bx+c=k有两个不相等的实数根,写出 k的取值范围;
(3)当0<x<3 时,写出函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.
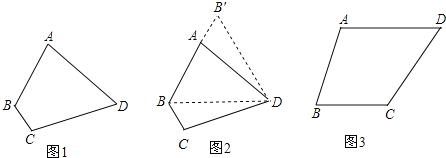
【尝试解决】
旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,则△BDB′的形状是 .
(2)在(1)的基础上,求四边形ABCD的面积.
[类比应用]如图3,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=2,BC=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
考点:几何变换综合题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=x2+ ( 2k-1)x+k+1的图象与x轴相交于O、A两点,
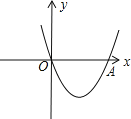
(1)求这个二次函数的解析式
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6.求点B的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,⊙O是△ABC的内切圆,切点分别为D、E、F.
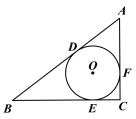
(1)已知∠C=90°.
①若BD=6,AD=4,则⊙O的半径r为 ,△ABC的面积为 ;
②若BD=m,AD=n,请用含m、n的代数式表示△ABC的面积;
(2)若![]() ,试判断△ABC的形状,并说明理由。
,试判断△ABC的形状,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com