
【题目】已知:如图,二次函数y=x2+ ( 2k-1)x+k+1的图象与x轴相交于O、A两点,
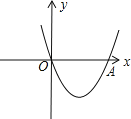
(1)求这个二次函数的解析式
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6.求点B的坐标。
【答案】(1)![]() ;(2)B点坐标是(4,4).
;(2)B点坐标是(4,4).
【解析】
(1)直接把原点坐标代入y=x2+(2k-1)x+k+1求出k的值,即可得到二次函数解析式;
(2)先确定A(3,0)和抛物线的对称轴,设B(m,n),再根据三角形面积公式得到![]() ,求出n值代入二次函数的解析式,即可求出点B坐标.
,求出n值代入二次函数的解析式,即可求出点B坐标.
(1)∵抛物线过原点O ,
∴k+1=0 ,
∴k=-1,
∴抛物线的解析式是![]() .
.
(2)令y=0,得x2-3x=0,
解得:x1=0,x2=3 ,
∴A(3,0) ,
∴OA=3 ,
设点B的坐标是(m,n),
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
当n=-4时,x2-3x= -4,此方程无解;
当n=4时,x2-3x=4,解得:x1=4,x2=-1,
∵对称轴x=![]() ,点B在对称轴右侧
,点B在对称轴右侧
∴x=4 ,
将x=4代入y=x2-3x.,得y=42-3![]() 4=4,
4=4,
∴B点坐标是(4,4).


科目:初中数学 来源: 题型:
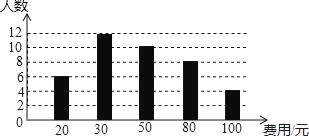
【题目】在全民读书月活动中,某校随机调查了部分同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题.
(1)这次调查获取的样本容量是 .(直接写出结果)
(2)这次调查获取的样本数据的众数是 ,中位数是 .(直接写出结果)
(3)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
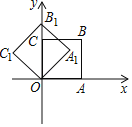
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y= ax2+bx+c(a≠0)对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),与y轴交点为(0,3),其部分图象如图所示,则下列结论错误的是( )
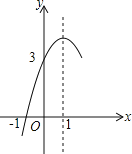
A.a-b+c=0B.关于x的方程ax2+bx+c- 3=0有两个不相等的实数根
C.abc>0D.当y>0时,-1<x<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A,B(点A在点B的左侧)
(1)当a=﹣1时,求A,B两点的坐标;
(2)过点P(3,0)作垂直于x轴的直线l,交抛物线于点C.当a=2时,求PB+PC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
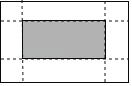
【题目】如图,有一张矩形纸片,长15cm,宽9cm,在它的四角各剪去一个同样的小正方形,然折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是48cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人:
(1)第一轮后患病的人数为 ;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com