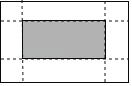
【题目】如图，有一张矩形纸片，长15cm，宽9cm，在它的四角各剪去一个同样的小正方形，然折叠成一个无盖的长方体纸盒．若纸盒的底面（图中阴影部分）面积是48cm2，求剪去的小正方形的边长．设剪去的小正方形边长是xcm，根据题意可列方程为_____．
一本好题口算题卡系列答案科目：初中数学 来源： 题型：
【题目】先阅读短文，然后回答短文后面所给出的问题：对于三个数a，b，c的平均数，最小的数都可以符号来表示，我们规定M{a，b，c}表示这三个数的平均数，min{a，b，c}表示这三个数中最小的数，max{a，b，c}表示这三个数中最大的数.例如：M{1，2，3}=
，min{1，2，3}=1，max{1，2，3}=3，M{1，2，a}=
=
.
(1)请填空：min{1，3，2}=___________.若x<0，则max{2，(x+1)2+2，x+1}=__________.
(2)若M{2x24x5，72，x2+10x7}=max{10，2x2+4x+12，8}，求x的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知:如图，二次函数y=x2+ ( 2k-1)x+k+1的图象与x轴相交于O、A两点，
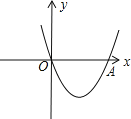
(1)求这个二次函数的解析式
(2)在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6.求点B的坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE，连接CD，BE．
（1）求证：∠AEB=∠ADC；
（2）连接DE，若∠ADC=105°，求∠BED的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
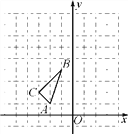
【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(－2，1)，B(－1，4)，C(－3，2)．
(1)以原点O为位似中心，相似比为1∶2，在y轴的左侧，画出△ABC放大后的图形△A1B1C1，并直接写出C1点的坐标；
(2)若点D(a，b)在线段AB上，请直接写出经过(1)的变化后点D的对应点D1的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y＝ax2+bx+c（a≠0）中的x与y的部分对应值如下表：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
给出以下结论：（1）二次函数y＝ax2+bx+c有最小值，最小值为﹣3；（2）当﹣
＜x＜2时，y＜0；（3）已知点A（x1，y1）、B（x2，y2）在函数的图象上，则当﹣1＜x1＜0，3＜x2＜4时，y1＞y2．上述结论中正确的结论个数为（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，AE：EB=1:2，DE交于点F.
（1）求AE：DC的值.
（2）△AEF与△CDF相似吗？若相似，求出相似比，请说明理由.
（3）如果
，求
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，⊙O是△ABC的内切圆，切点分别为D、E、F．
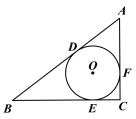
（1）已知∠C＝90°．
①若BD＝6，AD＝4，则⊙O的半径r为 ，△ABC的面积为 ；
②若BD＝m，AD＝n，请用含m、n的代数式表示△ABC的面积；
（2）若
，试判断△ABC的形状，并说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，BD平分∠ABC，
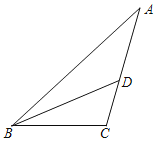
（1）按如下步骤作图：（保留作图痕迹）
第一步，分别以点B、D为圆心，以大于
BD的长为半径在BD两侧作弧，交于两点M、N；
第二步，连接MN分别交AB，BC于点E、F；
第三步，连接DE，DF．
（2）求证：四边形BEDF是菱形；
（3）若AD＝6，BF＝4，CD＝3，求AE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
