练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数y＝ax2+bx+c（a≠0）中的x与y的部分对应值如下表：

    x

    …

    ﹣3

    ﹣2

    ﹣1

    0

    1

    2

    3

    4

    …

    y

    …

    12

    5

    0

    ﹣3

    ﹣4

    ﹣3

    0

    5

    …

    给出以下结论：（1）二次函数y＝ax2+bx+c有最小值，最小值为﹣3；（2）当﹣＜x＜2时，y＜0；（3）已知点A（x1，y1）、B（x2，y2）在函数的图象上，则当﹣1＜x1＜0，3＜x2＜4时，y1＞y2．上述结论中正确的结论个数为（　　）

    A.0B.1C.2D.3

    【答案】B

    【解析】

    根据表格的数据，以及二次函数的性质，即可对每个选项进行判断.

    解：（1）函数的对称轴为：x＝1，最小值为﹣4，故错误，不符合题意；

    （2）从表格可以看出，当﹣＜x＜2时，y＜0，符合题意；

    （3）﹣1＜x1＜0，3＜x2＜4时，x2离对称轴远，故错误，不符合题意；

    故选择：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）如图①，在中，，，，则的值是_______．

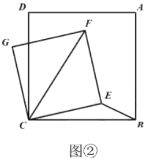
    （2）如图②，在正方形中，，点是平面上一动点，且，连接，在上方作正方形，求线段的最大值．

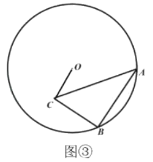
    问题解决：（3）如图③，半径为6，在中，，点在上，点在内，且．当点在圆上运动时，求线段的最小值．

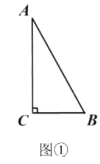
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“互联网+”时代，网上购物备受消费者青睐，某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可售价100条．为了吸引更多顾客，该网店采取降价措施．据市场调查反映：销售单价每降元，则每月可多销售5条．设每条裤子的售价为元(为正整数)，每月的销售量为条．

    （1）直接写出与的函数关系式；

    （2）设该网店每月获得的利润为元，当销售单价为多少元时，每月获得的利润最大，最大利润是多少？

    （3）该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生，为了保证捐款后每月利润不低于3800元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题）用n个2×1矩形，镶嵌一个2×n矩形，有多少种不同的镶嵌方案？（2×n矩形表示矩形的邻边是2和n）

    （探究）不妨假设有an种不同的镶嵌方案．为探究an的变化规律，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进，最后猜想得出结论．

    探究一：用1个2×1矩形，镶嵌一个2×1矩形，有多少种不同的镶嵌方案？

    如图（1），显然只有1种镶嵌方案．所以，a1＝1．

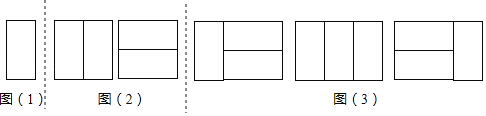
    探究二：用2个2×1矩形，镶嵌一个2×2矩形，有多少种不同的镶嵌方案？

    如图（2），显然只有2种镶嵌方案．所以，a2＝2．

    探究三：用3个2×1矩形，镶嵌一个2×3矩形，有多少种不同的镶嵌方案？

    一类：在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形，有1种镶嵌方案；

    二类：在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形，有2种镶嵌方案；

    如图（3）．所以，a3＝1+2＝3．

    探究四：用4个2×1矩形，镶嵌一个2×4矩形，有多少种不同的镶嵌方案？

    一类：在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形，有　 　种镶嵌方案；

    二类：在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形，有　 　种镶嵌方案；

    所以，a4＝　 　．

    探究五：用5个2×1矩形，镶嵌一个2×5矩形，有多少种不同的镶嵌方案？

    （仿照上述方法，写出探究过程，不用画图）

    ……

    （结论）用n个2×1矩形，镶嵌一个2×n矩形，有多少种不同的镶嵌方案？

    （直接写出an与an﹣1，an﹣2的关系式，不写解答过程）．

    （应用）用10个2×1矩形，镶嵌一个2×10矩形，有　 　种不同的镶嵌方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

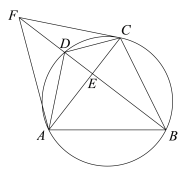
    【题目】如图，四边形ABCD内接于⊙O，AB=AC，BD⊥AC，垂足为E，点F在BD的延长线上，且DF=DC，连接AF、CF.

    (1)求证：∠BAC=2∠DAC；

    (2)若AF＝10，BC＝4，求tan∠BAD的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在中，，，，点由点出发沿方向向点匀速运动，同时点由点出发沿方向向点匀速运动，它们的速度均为．连接，设运动时间为．

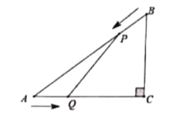
    （1）当为何值时，？

    （2）设的面积为，求与的函数关系式，并求出当为何值时，取得最大值？的最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一幅长20cm、宽12cm的图案，如图，其中有一横两竖的彩条，横、竖彩条的宽度比为3：2．设竖彩条的宽度为xcm，图案中三条彩条所占面积为ycm2．

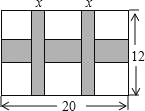
    （1）求y与x之间的函数关系式；

    （2）若图案中三条彩条所占面积是图案面积的，求横、竖彩条的宽度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

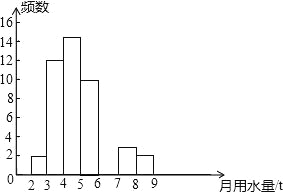
    【题目】小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）

    月均用水量（单位：t）

    频数

    百分比

    2≤x＜3

    2

    4%

    3≤x＜4

    12

    24%

    4≤x＜5

    a

    b

    5≤x＜6

    10

    20%

    6≤x＜7

    c

    12%

    7≤x＜8

    3

    6%

    8≤x＜9

    2

    4%

    （1）频数分布表中a= ，b= ．（填百分比），c= ；补全频数分布直方图．

    （2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有 户；

    （3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某旅行团32人在景区A游玩，他们由成人、少年和儿童组成．已知儿童10人，成人比少年多12人．

    （1）求该旅行团中成人与少年分别是多少人?

    （2）因时间充裕，该团准备让成人和少年（至少各1名）带领10名儿童去另一景区B游玩．景区B的门票价格为100元/张，成人全票，少年8折，儿童6折，一名成人可以免费携带一名儿童．

    ①若由成人8人和少年5人带队，则所需门票的总费用是多少元?

    ②若剩余经费只有1200元可用于购票，在不超额的前提下，最多可以安排成人和少年共多少人带队?求所有满足条件的方案，并指出哪种方案购票费用最少．

    查看答案和解析>>

    同步练习册答案