
【题目】(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值是_______.
的值是_______.
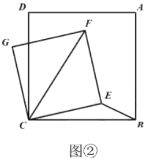
(2)如图②,在正方形![]() 中,
中,![]() ,点
,点![]() 是平面上一动点,且
是平面上一动点,且![]() ,连接
,连接![]() ,在
,在![]() 上方作正方形
上方作正方形![]() ,求线段
,求线段![]() 的最大值.
的最大值.
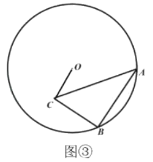
问题解决:(3)如图③,![]() 半径为6,在
半径为6,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 内,且
内,且![]() .当点
.当点![]() 在圆上运动时,求线段
在圆上运动时,求线段![]() 的最小值.
的最小值.
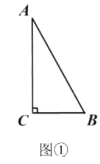
【答案】(1)![]() ;(2)
;(2)![]() ;(3)3
;(3)3
【解析】
(1)根据勾股定理算出AC,再根据正切的定义可得结果;
(2)根据题意得出当![]() 三点共线,且
三点共线,且![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值,即此时CF最大;
取得最大值,即此时CF最大;
(3)作![]() 的外接圆
的外接圆![]() ,连接
,连接![]() ,设
,设![]() 交劣弧
交劣弧![]() 于点
于点![]() ,则
,则![]() ,可得当点
,可得当点![]() 与点
与点![]() 重合时,线段
重合时,线段![]() 取得最小值,延长
取得最小值,延长![]() 交圆
交圆![]() 于点
于点![]() ,连接
,连接![]() ,证明
,证明![]() 得出
得出![]() ,从而可得
,从而可得![]() ,根据
,根据![]() ,在△ABF中,利用勾股定理列出方程,解得AC2,在△AOC中,求出OC即可.
,在△ABF中,利用勾股定理列出方程,解得AC2,在△AOC中,求出OC即可.
解:(1)∵![]() ,
,![]() ,
,![]() ,
,
∴AC=![]() ,
,
∴tanA=![]() ;
;
(2)![]() ,点
,点![]() 为定点,
为定点,
![]() 点
点![]() 在以
在以![]() 为圆心,
为圆心,![]() 长为半径的圆上运动.
长为半径的圆上运动.
![]() 当
当![]() 三点共线,且
三点共线,且![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值,
取得最大值,
![]() 在正方形
在正方形![]() 中,
中,![]() ,
,
![]() 最大=5+2=7,
最大=5+2=7,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() 线段
线段![]() 的最大值为
的最大值为![]() ;
;
(3)如图①,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 在
在![]() 中
中![]() ,且
,且![]() ,
,
![]() 的大小不变.
的大小不变.
又![]() 点
点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 内,且
内,且![]() 的半径为6,
的半径为6,
![]() 的大小,弦
的大小,弦![]() 的长均为定值.
的长均为定值.
作![]() 的外接圆
的外接圆![]() ,则点
,则点![]() 在劣弧
在劣弧![]() 上(不包括端点
上(不包括端点![]() ),
),

如图②,连接![]() ,设
,设![]() 交劣弧
交劣弧![]() 于点
于点![]() ,则
,则![]() ,且当点
,且当点![]() 与点
与点![]() 重合时,线段
重合时,线段![]() 取得最小值.
取得最小值.
延长![]() 交圆
交圆![]() 于点
于点![]() ,连接
,连接![]() ,
,
![]() ,
,
![]() 经过点
经过点![]() ,
,
![]() ,点
,点![]() 在
在![]() 上,
上,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() 在
在![]() 中,
中,![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() 线段
线段![]() 的最小值是3.
的最小值是3.



 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=8,BC=12,点E是边BC上一点,BE=5,点F是射线BA上一动点,连接EF,将△BEF沿着EF折叠,使B点的对应点P落在长方形一边的垂直平分线上,连接BP,则BP的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点O为圆心,OE为半径作优弧EF,连接OE,OF,且OE=3,∠EOF=120°,在弧EF上任意取点A,B(点B在点A的顺时针方向)且使AB=2,以AB为边向弧内作正三角形ABC.
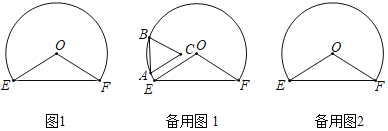
(1)发现:不论点A在弧上什么位置,点C与点O的距离不变,点C与点O的距离是 ;点C到直线EF的最大距离是 .
(2)思考:当点B在直线OE上时,求点C到OE的距离,在备用图1中画出示意图,并写出计算过程.
(3)探究:当BC与OE垂直或平行时,直接写出点C到OE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图
等级 | 成绩(得分) | 频数(人数) | 频率 |
A | 9~10分 | x | m |
B | 8~7 | 23 | 0.46 |
C | 6~5 | y | n |
D | 5分以下 | 3 | 0.06 |
(1)试直接写出x,y,m,n的值;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生400名,试估计这400名男生中成绩达到A等和B等的人数共有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年伊始,全国发生了传播速度快、感染范围广、防控难度大的新冠肺炎疫情.根据教育部提出的2020年春节延期开学,“停课不停学”的相关要求,很多学校开展了线上授课相关工作.为了更好地提高学生线上授课的效果,某中学进行了线上授课问卷调查.其中一项调查是:你认为影响师生互动的最主要因素是A.教师的授课理念;B.网络配麦等硬件问题;C.科目特点;D.学生的配合情况,针对这个题目,问卷时要求每位同学必须且只能选择其中一项.现随机抽取了若干名学生的调查问卷,将所得数据进行整理,制成如下条形统计图和扇形统计图.
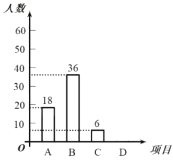
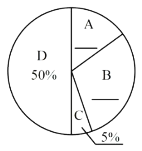
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生中认为影响师生互动最主要因素的众数为____________;
(3)已知该校有2400名学生,请你估计该校学生中认为影响师生互动的最主要因素是“C.科目特点”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“雪龙”号考察船在某海域进行科考活动,在点 A 处测得小岛C 在它的东北方向上,它沿南偏东37°方向航行 2 海里到达点 B 处,又测得小岛C 在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点 B 处与小岛C 之间的距离.(参考数据: sin22°0.37 , cos22°0.93 , tan 22° 0.40 ,![]() 1.4 ,
1.4 ,![]() 1.7 )
1.7 )
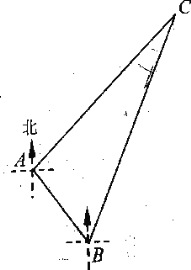
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )

A. 4![]() B. 6 C. 3
B. 6 C. 3![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①过三点可以确定一个圆
②直角三角形的两条直角边长分别是5和12,那么它的外接圆半径为6.5
③如果两个半径为2厘米和3厘米的圆相切,那么圆心距为5厘米
④三角形的重心到三角形三边的距离相等.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
给出以下结论:(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;(2)当﹣![]() <x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
<x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com