
【题目】如图,以点O为圆心,OE为半径作优弧EF,连接OE,OF,且OE=3,∠EOF=120°,在弧EF上任意取点A,B(点B在点A的顺时针方向)且使AB=2,以AB为边向弧内作正三角形ABC.
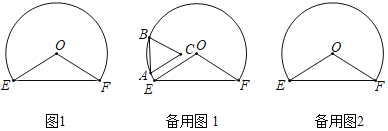
(1)发现:不论点A在弧上什么位置,点C与点O的距离不变,点C与点O的距离是 ;点C到直线EF的最大距离是 .
(2)思考:当点B在直线OE上时,求点C到OE的距离,在备用图1中画出示意图,并写出计算过程.
(3)探究:当BC与OE垂直或平行时,直接写出点C到OE的距离.
【答案】(1)![]() ;
;![]() ;(2)示意图见解析,点C到OE的距离为
;(2)示意图见解析,点C到OE的距离为![]() ;(3)当BC与OE垂直或平行时,点C到OE的距离为
;(3)当BC与OE垂直或平行时,点C到OE的距离为![]() 或
或![]() .
.
【解析】
(1)连接OB,OA,再连接OC并延长交AB于点G, 易知GO为线段AB的垂直平分线,通过勾股定理分别计算CG,GO的长,得到CO=GO-CG为定值即可;延长CO交EF于点H,当CO⊥EF时,点C到直线EF的距离最大,最大距离为CH的长,且CH=CO+OH,只需计算OH即可求出最大距离CH的长;
(2)过点C作OE的垂线,垂足为M,易证△OCM∽△OBG,得到![]() ,从而得到CM的长,即为点C到OE的距离;
,从而得到CM的长,即为点C到OE的距离;
(3)因为OC长不变,已求得,当BC与OE垂直或平行时,过点C作OE的垂线,利用OC不变,通过解相应的直角三角形,得到点C到OE的距离.
解:(1)如图1,连接OA、OB、OC,延长OC交AB于点G,
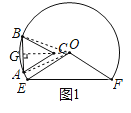
在正三角形ABC中,AB=BC=AC=2,
∵OA=OB,AC=BC,
∴OC垂直平分AB,
∴AG=![]() AB=1,
AB=1,
∴在Rt△AGC中,由勾股定理得:CG=![]() ,
,
在Rt△AGO中,由勾股定理得:OG=![]() ,
,
∴OC=![]() ;
;
如图2,延长CO交EF于点H,
当CO⊥EF时,点C到直线EF的距离最大,最大距离为CH的长,
∵OE=OF,CO⊥EF,
∴CO平分∠EOF,
∵∠EOF=120°,
∴∠EOH=![]() ∠EOF=60°,
∠EOF=60°,
在Rt△EOH中,cos∠EOH=![]() ,
,
∴cos60°=![]() =
=![]() ,
,
∴OH=![]() ,
,
∴CH=CO+OH=![]() ,
,
∴点C到直线EF的最大距离是![]() .
.
故答案为:![]() ;
;![]() .
.
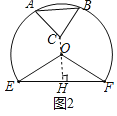
(2)如图3,当点B在直线OE上时,过点C作OE的垂线,垂足为M
由OA=OB,CA=CB可知,
点O,C都在线段AB的垂直平分线上,
过点C作AB的垂线,垂足为G,
则G为AB中点,直线CG过点O.
∴由∠COM=∠BOG,∠CMO=∠BGO
∴△OCM∽△OBG,
∴![]() ,
,
∴![]() ,
,
∴CM=![]() ,
,
∴点C到OE的距离为![]() .
.
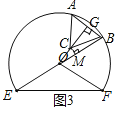
(3)如图4,当BC⊥OE时,设垂足为点M,
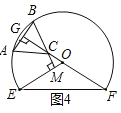
∵∠EOF=120°,
∴∠COM=180°﹣120°=60°,
∴在Rt△COM中,sin∠COM=![]() ,
,
∴sin60°=![]() =
=![]() ,
,
∴CM=![]() CO=
CO=![]() (
(![]() )=
)=![]() ;
;
如图5,当BC∥OE时,过点C作CN⊥OE,垂足为N,
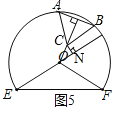
∵BC∥OE,
∴∠CON=∠GCB=30°,
∴在Rt△CON中,sin∠CON=![]() ,
,
∴sin30°=![]() =
=![]() ,
,
∴CN=![]() CO=
CO=![]() (
(![]() )=
)=![]() ;
;
综上所述,当BC与OE垂直或平行时,点C到OE的距离为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】学校餐厅中,一张桌子可坐6人,现有以下两种摆放方式:
(1)当有5张桌子时,第一种方式能坐 人,第二种方式能坐 人.
(2)当有n张桌子时,第一种方式能坐 人,第二种方式能坐 人.
(3)新学期有200人在学校就餐,但餐厅只有60张这样的餐桌,若你是老师,你打算选择以下哪种方式来摆放餐桌?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 点
点![]() 与点
与点![]() 在
在![]() 的同侧,且
的同侧,且![]() .
.

(1)如图1,点![]() 不与点
不与点![]() 重合,连结
重合,连结![]() 交
交![]() 于点
于点![]() .设
.设![]() 求
求![]() 关于
关于![]() 的函数解析式,写出自变量
的函数解析式,写出自变量![]() 的取值范围;
的取值范围;
(2)是否存在点![]() ,使
,使![]() 与
与![]() 相似,若存在,求
相似,若存在,求![]() 的长;若不存在,请说明理由;
的长;若不存在,请说明理由;
(3)如图2,过点![]() 作
作![]() 垂足为
垂足为![]() .将以点
.将以点![]() 为圆心,
为圆心,![]() 为半径的圆记为
为半径的圆记为![]() .若点
.若点![]() 到
到![]() 上点的距离的最小值为
上点的距离的最小值为![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台![]() 型电脑和
型电脑和![]() 型打印机.如果购买1台
型打印机.如果购买1台![]() 型电脑,2台
型电脑,2台![]() 型打印机,一共需要花费6200元;如果购买2台
型打印机,一共需要花费6200元;如果购买2台![]() 型电脑,1台
型电脑,1台![]() 型打印机,一共需要花费7900元.
型打印机,一共需要花费7900元.
(1)求每台![]() 型电脑和每台
型电脑和每台![]() 型打印机的价格分别是多少元?
型打印机的价格分别是多少元?
(2)如果学校购买![]() 型电脑和
型电脑和![]() 型打印机的预算费用不超过20000元,并且购买
型打印机的预算费用不超过20000元,并且购买![]() 型打印机的台数要比购买
型打印机的台数要比购买![]() 型电脑的台数多1台,那么该学校至多能购买多少台
型电脑的台数多1台,那么该学校至多能购买多少台![]() 型打印机?
型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
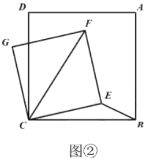
【题目】(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值是_______.
的值是_______.
(2)如图②,在正方形![]() 中,
中,![]() ,点
,点![]() 是平面上一动点,且
是平面上一动点,且![]() ,连接
,连接![]() ,在
,在![]() 上方作正方形
上方作正方形![]() ,求线段
,求线段![]() 的最大值.
的最大值.
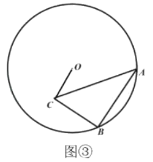
问题解决:(3)如图③,![]() 半径为6,在
半径为6,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 内,且
内,且![]() .当点
.当点![]() 在圆上运动时,求线段
在圆上运动时,求线段![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐,某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可售价100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降![]() 元,则每月可多销售5条.设每条裤子的售价为
元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润不低于3800元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com