练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列命题中正确的个数是（ ）

    ①过三点可以确定一个圆

    ②直角三角形的两条直角边长分别是5和12，那么它的外接圆半径为6.5

    ③如果两个半径为2厘米和3厘米的圆相切，那么圆心距为5厘米

    ④三角形的重心到三角形三边的距离相等．

    A.1个B.2个C.3个D.4个

    【答案】A

    【解析】

    ①根据圆的作法即可判断；

    ②先利用勾股定理求出斜边的长度，然后根据外接圆半径等于斜边的一半即可判断；

    ③根据圆与圆的位置关系即可得出答案；

    ④根据重心的概念即可得出答案．

    ①过不在同一条直线上的三点可以确定一个圆，故错误；

    ②∵直角三角形的两条直角边长分别是5和12，

    ∴斜边为 ,

    ∴它的外接圆半径为，故正确；

    ③如果两个半径为2厘米和3厘米的圆相切，那么圆心距为5厘米或1厘米，故错误；

    ④三角形的内心到三角形三边的距离相等，故错误；

    所以正确的只有1个，

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商场用36000元购进甲、乙两种商品，销售完后共获利6000元．其中甲种商品每件进价120元，售价138元；乙种商品每件进价100元，售价120元．

    （1）该商场购进甲、乙两种商品各多少件？

    （2）商场第二次以原进价购进甲、乙两种商品，购进乙种商品的件数不变，而购进甲种商品的件数是第一次的2倍，甲种商品按原售价出售，而乙种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于8160元，乙种商品最低售价为每件多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图①，在中，，，，则的值是_______．

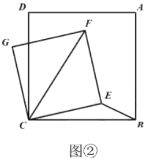
    （2）如图②，在正方形中，，点是平面上一动点，且，连接，在上方作正方形，求线段的最大值．

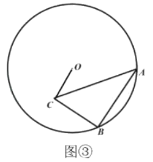
    问题解决：（3）如图③，半径为6，在中，，点在上，点在内，且．当点在圆上运动时，求线段的最小值．

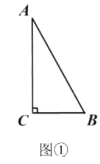
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，AB为直径， OD∥BC交⊙O于点D，交AC于点E，连接AD，BD，CD．

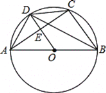
    （1）求证：AD=CD；

    （2）若AB=10，cos∠ABC=，求tan∠DBC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

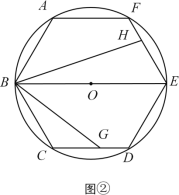
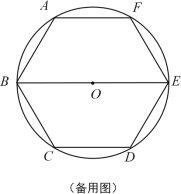
    【题目】如图，已知圆O是正六边形ABCDEF外接圆，直径BE=8，点G、H分别在射线CD、EF上（点G不与点C、D重合），且∠GBH=60°，设CG=x，EH=y．

    （1）如图①，当直线BG经过弧CD的中点Q时，求∠CBG的度数；

    （2）如图②，当点G在边CD上时，试写出y关于x的函数关系式，并写出x的取值范围；

    （3）联结AH、EG，如果△AFH与△DEG相似，求CG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“互联网+”时代，网上购物备受消费者青睐，某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可售价100条．为了吸引更多顾客，该网店采取降价措施．据市场调查反映：销售单价每降元，则每月可多销售5条．设每条裤子的售价为元(为正整数)，每月的销售量为条．

    （1）直接写出与的函数关系式；

    （2）设该网店每月获得的利润为元，当销售单价为多少元时，每月获得的利润最大，最大利润是多少？

    （3）该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生，为了保证捐款后每月利润不低于3800元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题）用n个2×1矩形，镶嵌一个2×n矩形，有多少种不同的镶嵌方案？（2×n矩形表示矩形的邻边是2和n）

    （探究）不妨假设有an种不同的镶嵌方案．为探究an的变化规律，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进，最后猜想得出结论．

    探究一：用1个2×1矩形，镶嵌一个2×1矩形，有多少种不同的镶嵌方案？

    如图（1），显然只有1种镶嵌方案．所以，a1＝1．

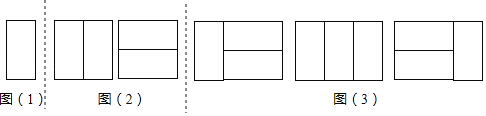
    探究二：用2个2×1矩形，镶嵌一个2×2矩形，有多少种不同的镶嵌方案？

    如图（2），显然只有2种镶嵌方案．所以，a2＝2．

    探究三：用3个2×1矩形，镶嵌一个2×3矩形，有多少种不同的镶嵌方案？

    一类：在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形，有1种镶嵌方案；

    二类：在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形，有2种镶嵌方案；

    如图（3）．所以，a3＝1+2＝3．

    探究四：用4个2×1矩形，镶嵌一个2×4矩形，有多少种不同的镶嵌方案？

    一类：在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形，有　 　种镶嵌方案；

    二类：在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形，有　 　种镶嵌方案；

    所以，a4＝　 　．

    探究五：用5个2×1矩形，镶嵌一个2×5矩形，有多少种不同的镶嵌方案？

    （仿照上述方法，写出探究过程，不用画图）

    ……

    （结论）用n个2×1矩形，镶嵌一个2×n矩形，有多少种不同的镶嵌方案？

    （直接写出an与an﹣1，an﹣2的关系式，不写解答过程）．

    （应用）用10个2×1矩形，镶嵌一个2×10矩形，有　 　种不同的镶嵌方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

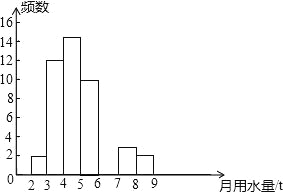
    【题目】小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）

    月均用水量（单位：t）

    频数

    百分比

    2≤x＜3

    2

    4%

    3≤x＜4

    12

    24%

    4≤x＜5

    a

    b

    5≤x＜6

    10

    20%

    6≤x＜7

    c

    12%

    7≤x＜8

    3

    6%

    8≤x＜9

    2

    4%

    （1）频数分布表中a= ，b= ．（填百分比），c= ；补全频数分布直方图．

    （2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有 户；

    （3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率．

    查看答案和解析>>

    同步练习册答案