
����Ŀ�������⣩��n��2��1���Σ���Ƕһ��2��n���Σ��ж����ֲ�ͬ����Ƕ��������2��n���α�ʾ���ε��ڱ���2��n��
��̽��������������an�ֲ�ͬ����Ƕ������Ϊ̽��an�ı仯���ɣ����Dz�ȡһ���������⻯�IJ��ԣ��ȴ�����������֣�����εݽ���������ó����ۣ�
̽��һ����1��2��1���Σ���Ƕһ��2��1���Σ��ж����ֲ�ͬ����Ƕ������
��ͼ��1������Ȼֻ��1����Ƕ���������ԣ�a1��1��
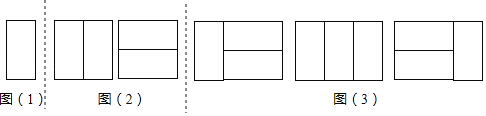
̽��������2��2��1���Σ���Ƕһ��2��2���Σ��ж����ֲ�ͬ����Ƕ������
��ͼ��2������Ȼֻ��2����Ƕ���������ԣ�a2��2��
̽��������3��2��1���Σ���Ƕһ��2��3���Σ��ж����ֲ�ͬ����Ƕ������
һ�ࣺ��̽��һÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ���1����Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ���2����Ƕ������
��ͼ��3�������ԣ�a3��1+2��3��
̽���ģ���4��2��1���Σ���Ƕһ��2��4���Σ��ж����ֲ�ͬ����Ƕ������
һ�ࣺ��̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ����� ������Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ����� ������Ƕ������
���ԣ�a4���� ����
̽���壺��5��2��1���Σ���Ƕһ��2��5���Σ��ж����ֲ�ͬ����Ƕ������
����������������д��̽�����̣����û�ͼ��
����
�����ۣ���n��2��1���Σ���Ƕһ��2��n���Σ��ж����ֲ�ͬ����Ƕ������
��ֱ��д��an��an��1��an��2�Ĺ�ϵʽ����д�����̣���
��Ӧ�ã���10��2��1���Σ���Ƕһ��2��10���Σ����� ���ֲ�ͬ����Ƕ������
���𰸡���1��2��3��5����2��an��an��1+an��2����3��89.
��������
̽���ģ���ͼ����˵����a4=2+3=5��
̽���壺ͬ����̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���κ�̽����ÿ����Ƕͼ���Ҳ���������Ƕ��1��2��1���Σ���ӿɵý��ۣ�
���ۣ�����̽���ĺ���ɵù��ɣ�an=an-1+an-2��
Ӧ�ã����ý������λ�������С��־��Ϊ5��4������̽���ĺ����ֵ����ɵý��ۣ�
�⣺̽���ģ�
��ͼ4��ʾ��

һ�ࣺ��̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ���2����Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ���3����Ƕ������
���ԣ�a4��2+3��5��
�ʴ�Ϊ2��3��5��
̽���壺
һ�ࣺ��̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ���3����Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ���5����Ƕ������
���ԣ�a5��3+5��8��
����
���ۣ�an��an��1+an��2��
Ӧ�ã�a10��a9+a8��a7+a8+a8��2a8+a7��2��a7+a6��+a7��3a7+2a6��3��a6+a5��+2a6��5a6+3a5��5��a5+a4��+3a5��8a5+5a4��8��8+5��5��89��
�ʴ�Ϊ89��


 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽���꼶����1000�׳��ܵijɼ������������ȡ��50���������в��ԣ����ݲ������ֱ��������ǵĵ÷ֽ���ͳ�ƺ��ΪA��B��C��D�ĵȣ������Ƴ������Ƶ���ֲ���������ͳ��ͼ
�ȼ� | �ɼ����÷֣� | Ƶ���������� | Ƶ�� |
A | 9��10�� | x | m |
B | 8��7 | 23 | 0.46 |
C | 6��5 | y | n |
D | 5������ | 3 | 0.06 |
��1����ֱ��д��x��y��m��n��ֵ��
��2�����ʾ�÷�ΪC�ȵ����ε�Բ�ĽǵĶ�����
��3�������У���꼶��������400�����Թ�����400�������гɼ��ﵽA�Ⱥ�B�ȵ��������ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ�ĸ����ǣ� ��
�ٹ��������ȷ��һ��Բ
��ֱ�������ε�����ֱ�DZ߳��ֱ���5��12����ô�������Բ�뾶Ϊ6.5
����������뾶Ϊ2����3����Բ���У���ôԲ�ľ�Ϊ5����
�������ε����ĵ����������ߵľ�����ȣ�
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+2x+c����A����1��0����B���㣬����y�ύ�ڵ�C��0��3������������ֱ��y����x��1����A��E���㣮
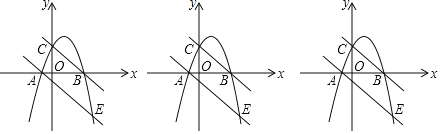
��1���������ߵĽ���ʽ��
��2�����������Ƿ����һ��Q��ʹ����AQE����AEΪ�ױߵĵ��������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
��3��P����x������λ�ڵ�B����࣬����P��B��CΪ���������������ABE���ƣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С���������ſ�Ƭ����Ϸ����Ƭ�Ϸֱ�д��A��B��B����Щ��Ƭ����ĸ����ȫ��ͬ�������������һ�ţ�������ĸ��Żأ����ϴ�Ⱥ��ٴ�������һ�ţ��������������Ƭ��ĸ��ͬ��С��ʤ������С��ʤ�������Ϸ��˫����ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
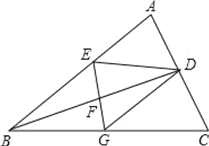
����Ŀ����ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ����Ĵ�ֱƽ���߷ֱ�AB��BC�ڵ�E��F��G������ED��DG��
��1�����ж��ı���EBGD����״����˵�����ɣ�
��2������ABC=30�㣬��C=45�㣬ED=2����GC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | �� |
y | �� | 12 | 5 | 0 | ��3 | ��4 | ��3 | 0 | 5 | �� |
�������½��ۣ���1�����κ���y��ax2+bx+c����Сֵ����СֵΪ��3����2������![]() ��x��2ʱ��y��0����3����֪��A��x1��y1����B��x2��y2���ں�����ͼ���ϣ���1��x1��0��3��x2��4ʱ��y1��y2��������������ȷ�Ľ��۸���Ϊ��������
��x��2ʱ��y��0����3����֪��A��x1��y1����B��x2��y2���ں�����ͼ���ϣ���1��x1��0��3��x2��4ʱ��y1��y2��������������ȷ�Ľ��۸���Ϊ��������
A.0B.1C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��չ�������ж�������������༶�μӸû������ͳ�ƽ�����±�����������ͳ�����ݣ�����˵������ȷ���ǣ���
�༶ | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� |
���� | 52 | 60 | 62 | 54 | 58 | 62 |
A.ƽ������58B.��λ����58C.������40D.������60
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��
��![]() ���㣬��A��������
���㣬��A��������![]() ����C��������
����C��������![]() ������P���������ϣ�
������P���������ϣ�
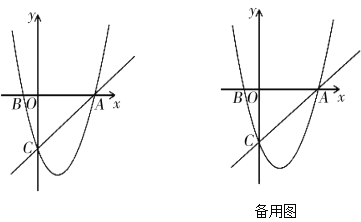
��1��b=___��c=____����B������Ϊ______��
��2���Ƿ���ڵ�P��ʹ��![]() ����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
��3��������P��PE��ֱy���ڵ�E����ֱ��AC�ڵ�D������D��x��Ĵ��ߣ�����ΪF������EF�����߶�EF�ij������ʱ�������P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com