
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��
��![]() ���㣬��A��������
���㣬��A��������![]() ����C��������
����C��������![]() ������P���������ϣ�
������P���������ϣ�
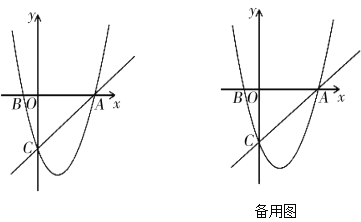
��1��b=___��c=____����B������Ϊ______��
��2���Ƿ���ڵ�P��ʹ��![]() ����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
��3��������P��PE��ֱy���ڵ�E����ֱ��AC�ڵ�D������D��x��Ĵ��ߣ�����ΪF������EF�����߶�EF�ij������ʱ�������P�����꣮
���𰸡���1��![]() ����2�����ڣ����ɼ�������P��������
����2�����ڣ����ɼ�������P��������![]() ��
��![]() ����3����
����3����![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��������
��1������A�͵�C��������������ߵĽ���ʽ�����b��c��ֵ��Ȼ����y=0����õ�B�����ꣻ
��2���ֱ����C�͵�A��AC�Ĵ��ߣ�����������P1��P2���������AC�Ľ���ʽ��Ȼ������P1C��P2A�Ľ���ʽ����������P1C��P2A�������ߵĽ������꼴�ɣ�
��3������OD����֤���ı���OEDFΪ���Σ��Ӷ��õ�OD=EF��Ȼ����ݴ��߶���̿���õ�D�������꣬�Ӷ��õ���P�������꣬Ȼ���������ߵĽ���ʽ����õ�P�����꣮
�⣺��1���߽���A�͵�C��������������ߵĽ���ʽ�ã�![]() ����ã�b=-2��c=-3��
����ã�b=-2��c=-3��
�������ߵĽ���ʽΪy=x2-2x-3��
����x2-2x-3=0����ã�x1=-1��x2=3��
���B��������-1��0����
�ʴ�Ϊ��-2��-3����-1��0����
��2�����ڣ�
���ɣ���ͼ��ʾ��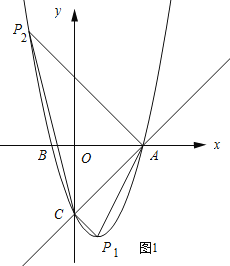
�ٵ���ACP1=90����
�ɣ�1����֪��A������Ϊ��3��0����
��AC�Ľ���ʽΪy=kx-3��
�߽���A����������3k-3=0�����k=1��
��ֱ��AC�Ľ���ʽΪy=x-3��
��ֱ��CP1�Ľ���ʽΪy=-x-3��
�߽�y=-x-3��y=x2-2x-3�������x1=1��x2=0����ȥ����
���P1��������1��-4����
�ڵ���P2AC=90��ʱ��
��AP2�Ľ���ʽΪy=-x+b��
�߽�x=3��y=0����ã�-3+b=0�����b=3��
��ֱ��AP2�Ľ���ʽΪy=-x+3��
�߽�y=-x+3��y=x2-2x-3�������x1=-2��x2=3����ȥ����
���P2��������-2��5����
����������P�������ǣ�1��-4����-2��5����
��3����ͼ2��ʾ������OD��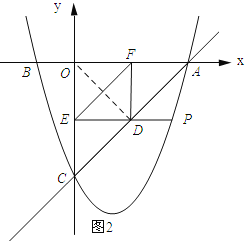
�������֪���ı���OFDE�Ǿ��Σ���OD=EF��
���ݴ��߶���̣��ɵõ�OD��ACʱ��OD��̣���EF��̣�
�ɣ�1����֪����Rt��AOC�У�
��OC=OA=3��OD��AC��
��D��AC���е㣮
�֡�DF��OC��
��DF��![]() ��
��
���P����������![]() ��
��
��x22x3��![]() ����ã�x��
����ã�x��![]() ��
��
�൱EF���ʱ����P�������ǣ���![]() ��
��![]() ����
����![]() ��
��![]() ����
����


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣩��n��2��1���Σ���Ƕһ��2��n���Σ��ж����ֲ�ͬ����Ƕ��������2��n���α�ʾ���ε��ڱ���2��n��
��̽��������������an�ֲ�ͬ����Ƕ������Ϊ̽��an�ı仯���ɣ����Dz�ȡһ���������⻯�IJ��ԣ��ȴ�����������֣�����εݽ���������ó����ۣ�
̽��һ����1��2��1���Σ���Ƕһ��2��1���Σ��ж����ֲ�ͬ����Ƕ������
��ͼ��1������Ȼֻ��1����Ƕ���������ԣ�a1��1��
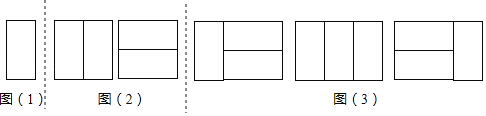
̽��������2��2��1���Σ���Ƕһ��2��2���Σ��ж����ֲ�ͬ����Ƕ������
��ͼ��2������Ȼֻ��2����Ƕ���������ԣ�a2��2��
̽��������3��2��1���Σ���Ƕһ��2��3���Σ��ж����ֲ�ͬ����Ƕ������
һ�ࣺ��̽��һÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ���1����Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ���2����Ƕ������
��ͼ��3�������ԣ�a3��1+2��3��
̽���ģ���4��2��1���Σ���Ƕһ��2��4���Σ��ж����ֲ�ͬ����Ƕ������
һ�ࣺ��̽����ÿ����Ƕͼ���Ҳ��ٺ�����Ƕ2��2��1���Σ����� ������Ƕ������
���ࣺ��̽����ÿ����Ƕͼ���Ҳ���������Ƕ1��2��1���Σ����� ������Ƕ������
���ԣ�a4���� ����
̽���壺��5��2��1���Σ���Ƕһ��2��5���Σ��ж����ֲ�ͬ����Ƕ������
����������������д��̽�����̣����û�ͼ��
����
�����ۣ���n��2��1���Σ���Ƕһ��2��n���Σ��ж����ֲ�ͬ����Ƕ������
��ֱ��д��an��an��1��an��2�Ĺ�ϵʽ����д�����̣���
��Ӧ�ã���10��2��1���Σ���Ƕһ��2��10���Σ����� ���ֲ�ͬ����Ƕ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
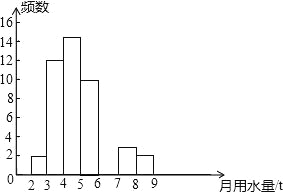
����Ŀ��С��ͬѧ��ѧУ��֯���������и����˽�������ס��С��450�������������ˮ�����������������������ɻ�������¾���ˮ������λ��t������������������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����ͼ��
�¾���ˮ������λ��t�� | Ƶ�� | �ٷֱ� |
2��x��3 | 2 | 4% |
3��x��4 | 12 | 24% |
4��x��5 | a | b |
5��x��6 | 10 | 20% |
6��x��7 | c | 12% |
7��x��8 | 3 | 6% |
8��x��9 | 2 | 4% |
��1��Ƶ���ֲ�����a= ��b= ������ٷֱȣ���c= ����ȫƵ���ֲ�ֱ��ͼ��
��2�������ͥ�¾���ˮ�������ڻ����4t��С��7t��Ϊ�е���ˮ����ͥ������ͨ���������������е��е���ˮ����ͥ��Լ�� ����
��3�����¾���ˮ����2��x��3��8��x��9��������Χ�ڵ�������ͥ�������ȡ2���������б�������״ͼ���ȡ����2����ͥ���Բ�ͬ��Χ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݽ��ܲ���ͳ�ƣ����ٹ�·������ʻ��������ͨ�¹ʵ���Ҫԭ������ijУ��ѧ����С��ļ���ͬѧ�볢�����Լ���ѧ��֪ʶ���٣���ǭ���ٹ�·ij·�ε������ǣ�ÿСʱ80ǧ�ף������ʱ�ٲ�����80ǧ�ף�����ͼ�����ǽ��۲�����ڵ���·l�ľ���Ϊ0.1ǧ��P������ʱ��һ���γ����뽭����������ֱ��ʻ������ô˳���A����ʻ��B�����õ�ʱ��Ϊ3�루ע��3�룽![]() Сʱ�����������APO��59������BPO��45�����Լ���AB���жϴ˳��Ƿ��٣�����ȷ��0.001�������ο����ݣ�sin59���0.8572��cos59���0.5150��tan59���1.6643��
Сʱ�����������APO��59������BPO��45�����Լ���AB���жϴ˳��Ƿ��٣�����ȷ��0.001�������ο����ݣ�sin59���0.8572��cos59���0.5150��tan59���1.6643��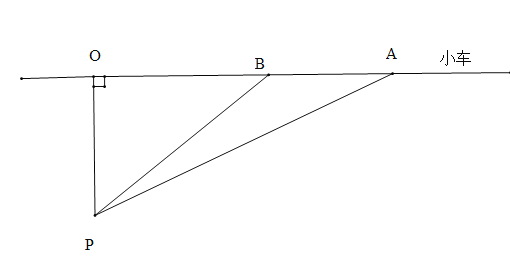
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽�ѧ��һѧ�����幤��ʱ���������ȫ��50��ѧ�����е��飬�����幤��ʱ��![]() ����λ��Сʱ������ѧ���ֳ����ࣺ
����λ��Сʱ������ѧ���ֳ����ࣺ ![]() �ࣨ
�ࣨ![]() ����
����![]() �ࣨ
�ࣨ![]() ����
����![]() �ࣨ
�ࣨ![]() ����
����![]() �ࣨ
�ࣨ![]() ����
����![]() �ࣨ
�ࣨ![]() �������Ƴ��в�����������ͳ��ͼ��ͼ11.
�������Ƴ��в�����������ͳ��ͼ��ͼ11.

����������Ϣ������������⣺
��1��![]() ��ѧ���� �ˣ���ȫ����ͳ��ͼ��
��ѧ���� �ˣ���ȫ����ͳ��ͼ��
��2��![]() ��ѧ������ռ�������������� %��
��ѧ������ռ�������������� %��
��3���Ӹð����幤ʱ����![]() ��ѧ������ѡ2�ˣ�����2�����幤ʱ�䶼��
��ѧ������ѡ2�ˣ�����2�����幤ʱ�䶼��![]() �еĸ�����
�еĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���һ���ѧ�ƻ�����![]() �����ͺŵ�С�ڰ壬��Ǣ̸�� ����һ��
�����ͺŵ�С�ڰ壬��Ǣ̸�� ����һ��![]() ��С�ڰ����һ��
��С�ڰ����һ��![]() ��С�ڰ��
��С�ڰ��![]() Ԫ���ҹ���
Ԫ���ҹ���![]() ��
��![]() ��С�ڰ��
��С�ڰ��![]() ��
��![]() ��С�ڰ干��
��С�ڰ干��![]() Ԫ��
Ԫ��
��1������һ��![]() ��С�ڰ��һ��
��С�ڰ��һ��![]() ��С�ڰ����Ҫ����Ԫ��
��С�ڰ����Ҫ����Ԫ��
��2������ѧУ��ʵ��������蹺��![]() �����ͺŵ�С�ڰ干
�����ͺŵ�С�ڰ干![]() �飬���ҹ���
�飬���ҹ���![]() ��С�ڰ�����������ڹ���
��С�ڰ�����������ڹ���![]() ��С�ڰ������������ѧУ��������С�ڰ�����Ҫ����Ԫ��
��С�ڰ������������ѧУ��������С�ڰ�����Ҫ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������32���ھ���A���棬�����ɳ��ˡ�����Ͷ�ͯ��ɣ���֪��ͯ10�ˣ����˱������12�ˣ�
��1������������г���������ֱ��Ƕ�����?
��2����ʱ���ԣ���������ó��˺����꣨���ٸ�1��������10����ͯȥ��һ����B���森����B����Ʊ�۸�Ϊ100Ԫ/�ţ�����ȫƱ������8�ۣ���ͯ6�ۣ�һ�����˿������Я��һ����ͯ��
�����ɳ���8�˺�����5�˴��ӣ���������Ʊ���ܷ����Ƕ���Ԫ?
����ʣ�ྭ��ֻ��1200Ԫ�����ڹ�Ʊ���ڲ������ǰ���£��������ų��˺����깲�����˴���?���������������ķ�������ָ�����ַ�����Ʊ�������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ�����У�һ��������3�֣���ʦ����ֻ�����������÷�ֻ��Ϊ0�֣�1�֣�2�֣�3�֣�����ʦΪ���˽�ѧ���÷���������������������Գ�����1��������ѧ������������˷����������������������в�������ͳ��ͼ����ͼ��ʾ��

����������⣺
��1��m= ��n= ������ȫ����ͳ��ͼ��
��2���ڳ�����1���������ȡһ��ѧ���ijɼ�������еijɼ�Ϊ�÷������ĸ��ʣ�
��3�������Ҳ���С֪ʶ����ͨ�������ж��������ڸð༶��˵��������һ���Ѷȵ����⣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC��D��E�ֱ��ڱ�AB��AC�ϣ����������У�����ȷ����ADE�ס�ACB���ǣ�������
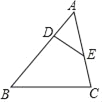
A. ��AED����B B. ��BDE+��C��180��
C. ADBC��ACDE D. ADAB��AEAC
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com