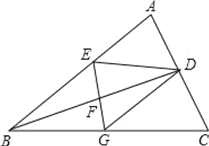
【题目】如图，BD是△ABC的角平分线，它的垂直平分线分别交AB、BC于点E、F、G，连接ED、DG．

（1）请判断四边形EBGD的形状，并说明理由；

（2）若∠ABC=30°，∠C=45°，ED=2，求GC的长．

参考答案：

【答案】（1）四边形EBGD是菱形．理由见解析；（2）1+

【解析】试题分析：（1）结论四边形EBGD是菱形．只要证明BE=ED=DG=GB即可．

（2）作DH⊥BC于H，由四边形EBGD为菱形ED=DG=2，求出GH，CH即可解决问题．

试题解析：（1）四边形EBGD是菱形．

理由：∵EG垂直平分BD，

∴EB=ED，GB=GD，

∴∠EBD=∠EDB，

∵∠EBD=∠DBC，

∴∠EDF=∠GBF，

在△EFD和△GFB中，

，

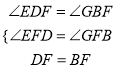∴△EFD≌△GFB，

∴ED=BG，

∴BE=ED=DG=GB，

∴四边形EBGD是菱形．

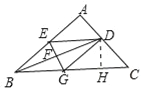
（2）作DH⊥BC于H，

∵四边形EBGD为菱形ED=DG=2，

∴∠ABC=30°，∠DGH=30°，

∴DH=1，GH=，

∵∠C=45°，

∴DH=CH=1，

∴CG=GH+CH=1+．

关闭