
【题目】如图,长方形ABCD中,AB=8,BC=12,点E是边BC上一点,BE=5,点F是射线BA上一动点,连接EF,将△BEF沿着EF折叠,使B点的对应点P落在长方形一边的垂直平分线上,连接BP,则BP的长是_____.

【答案】4![]() 或
或![]() 或2
或2![]()
【解析】
分三种情况:①当P落在AB边的垂直平分线上且F在BA的延长线上时;②当P落在AB边的垂直平分线上且F在BA上时;③当P落在BC边的垂直平分线上时;由折叠的性质和勾股定理即可得出答案.
解:分三种情况:①当P落在AB边的垂直平分线上时,如图1所示:
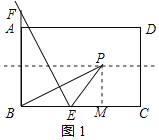
作PM⊥BC于M,则PM=![]() AB=4,∠PMB=90°,
AB=4,∠PMB=90°,
由折叠的性质得:PE=BE=5,
∴EM=![]() =3,
=3,
∴BM=BE+EM=8,
∴BP=![]() ;
;
②当P落在AB边的垂直平分线上,且F在线段BA上时,如图2所示:
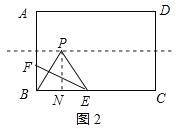
作PN⊥BC于N,则PN=![]() AB=4,∠PNB=90°,
AB=4,∠PNB=90°,
由折叠的性质得:PE=BE=5,
∴EN=![]() =3,
=3,
∴BN=BE-EN=2,
∴BP=![]() ;
;
③当P落在BC边的垂直平分线上时,如图3所示:
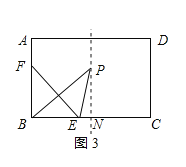
则BN=![]() BC=6,∠PNB=90°,
BC=6,∠PNB=90°,
由折叠的性质得:PE=BE=5,
∴EN=BN-BE=1,PN=![]() ,
,
∴BP=![]() ;
;
综上所述,BP的长是4![]() 或
或![]() 或2
或2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分别找一点M、N,使△AMN的周长最小时,∠AMN+∠ANM的度数为_______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到正方形AEGF(AE=EG=GF=AF,![]() ∠EAF=∠E=∠F=∠G=90°).
∠EAF=∠E=∠F=∠G=90°).

(1) 若AD=6,BD=2,求CG的长.
(2) 设BG=a,CG=b,BC=c.
①AE=_______.(用a、b、c表示)
②利用正方形面积验证勾股定理![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是
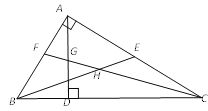
A.①②③④B.①②③C.②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.

(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“鄂”、“州”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“鄂”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com