
【题目】如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.

(1)求证:DP=DB;
(2)求证:DA+DB=DC;
【答案】(1)见解析;(2)见解析
【解析】
(1)首先由等边三角形的性质易得AB=AC=BC,由垂直平分线的性质易得AP=AC,等量代换可得AP=AB,由SAS定理可证得△PAD≌△BAD,利用全等三角形的性质可得结论;
(2)在CP上截CQ=PD,证明△ACQ≌△APD,等量代换,证得△ADQ为等边三角形,得出结论.
(1) ∵AH是PC的垂直平分线
∴PA=PC=AB
∵AD平分∠PAB
∴∠PAD=∠BAD
在△PAD和△BAD中,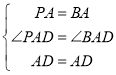
∴△PAD≌△BAD(SAS)
∴DP=DB
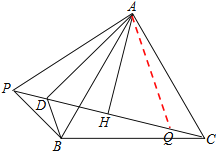
(2) 在CP上截取CQ=PD,连接AQ
∵AP=AC
∴∠APD=∠ACQ
在△APD和△ACQ中,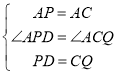
∴△APD≌△ACQ(SAS)
∴AD=AQ,∠CAQ=∠PAD
∴∠BAC=∠CAQ+∠BAQ=∠PAD+∠BAQ=∠BAD+∠BAQ=∠DAQ=60°
∴△ADQ为等边三角形
∴AD=DQ
∴CD=DQ+CQ=AD+DB


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 了解“孝感市初中生每天课外阅读书籍时间的情况”最适合的调查方式是全面调查
B. 甲乙两人跳绳各10次,其成绩的平均数相等,![]() ,则甲的成绩比乙稳定
,则甲的成绩比乙稳定
C. 三张分别画有菱形,等边三角形,圆的卡片,从中随机抽取一张,恰好抽到中心对称图形卡片的概率是![]()
D. “任意画一个三角形,其内角和是![]() ”这一事件是不可能事件
”这一事件是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
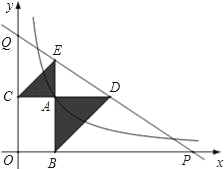
【题目】如图,已知动点A在函数y=![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=8,BC=12,点E是边BC上一点,BE=5,点F是射线BA上一动点,连接EF,将△BEF沿着EF折叠,使B点的对应点P落在长方形一边的垂直平分线上,连接BP,则BP的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,则∠F的度数为( )

A. 120° B. 135° C. 150° D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
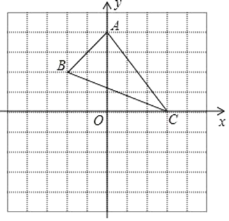
【题目】如图,已知A(0,4),B(﹣2,2),C(3,0).
(1)作△ABC关于x轴对称的△A1B1C1;
(2)求△A1B1C1的面积与A1B1边上的高;
(3)在x轴上有一点P,使PA+PB最小,求PA+PB的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com