
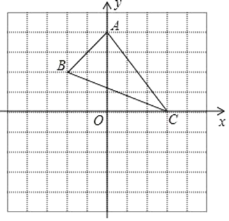
【题目】如图,已知A(0,4),B(﹣2,2),C(3,0).
(1)作△ABC关于x轴对称的△A1B1C1;
(2)求△A1B1C1的面积与A1B1边上的高;
(3)在x轴上有一点P,使PA+PB最小,求PA+PB的最小值.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.

(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.
(1)求证:BC=DE;
(2)连接AD、BE,若∠BAC=∠C,求证:四边形DBEA是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的个数是
①若代数式![]() 有意义,则x的取值范围为x≤1且x≠0.
有意义,则x的取值范围为x≤1且x≠0.
②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.
③若反比例函数![]() (m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
(m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y=x2中偶函数的个数为2个.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“鄂”、“州”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“鄂”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探究两个三角形满足两边和其中一边的对角对应相等(“SSA”)是否能判定两个三角形全等时,我们设计不同情形进行探究:
(1)例如,当∠B 是锐角时,如图 ,BC=EF,∠B=∠E,在射线 EM 上有点 D,使 DF=AC,用尺规画出符合条件的点 D,则△ABC 和△DEF 的关系是( );
A.全等 B. 不全等 C. 不一定全等

我们进一步发现如果能确定这两个三角形的形状,那么“SSA”是成立的.
(2)例如,已知:如图,在锐角△ABC 和锐角△DEF 中,AC=DF,BC=EF,∠B=∠E. 求证:△ABC≌△DEF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com