
【题目】如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为_______.

科目:初中数学 来源: 题型:
【题目】如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,则∠F的度数为( )

A. 120° B. 135° C. 150° D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t
(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了30分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有320米
其中正确的结论有( )

A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
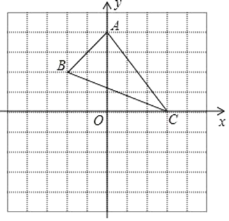
【题目】如图,已知A(0,4),B(﹣2,2),C(3,0).
(1)作△ABC关于x轴对称的△A1B1C1;
(2)求△A1B1C1的面积与A1B1边上的高;
(3)在x轴上有一点P,使PA+PB最小,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.

(1)求证:DE为⊙O的切线.
(2)求证:AB:AC=BF:DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从A地匀速驶往相距350km的B地,当货车行驶1小时经过途中的C地时,一辆快递车恰好从C地出发以另一速度匀速驶往B地,当快递车到达B地后立即掉头以原来的速度匀速驶往A地.(货车到达B地,快递车到达A地后分别停止运动)行驶过程中两车与B地间的距离y(单位:km)与货车从出发所用的时间x(单位:h)间的函数关系如图所示.则货车到达B地后,快递车再行驶_____h到达A地.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com