
【题目】已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.

(1)求证:DE为⊙O的切线.
(2)求证:AB:AC=BF:DF.
【答案】详见解析
【解析】
(1)连接OD、AD,求出CDA=∠BDA=90°,求出∠1=∠4,∠2=∠3,推出∠4+∠3=∠1+∠2=90°,根据切线的判定推出即可;
(2)证△ABD∽△CAD,刘![]() ,证△FAD∽△FDB,得
,证△FAD∽△FDB,得![]() ,即可得出AB:AC=BF:DF。
,即可得出AB:AC=BF:DF。
证明:(1)连接DO、DA,
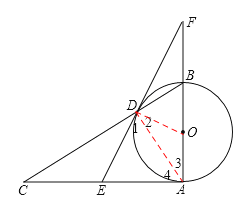
∵AB为⊙O直径,∴∠CDA=∠BDA=90°。
∵CE=EA,∴DE=EA。∴∠1=∠4。
∵OD=OA,∴∠2=∠3。
∵∠4+∠3=90°,∴∠1+∠2=90°,即:∠EDO=90°。
∴DE⊥OD。
∵OD是半径,∴DE为⊙O的切线。
(2)∵∠3+∠DBA=90°,∠3+∠4=90°,
∴∠4=∠DBA。
∵∠CDA=∠BDA=90°,∴△ABD∽△CAD。
∴![]() 。
。
∵∠FDB+∠BDO=90°,∠DBO+∠3=90°,
又∵OD=OB,∴∠BDO=∠DBO。∴∠3=∠FDB。
∵∠F=∠F,∴△FAD∽△FDB。∴![]() 。
。
∴![]() ,即AB:AC=BF:DF。
,即AB:AC=BF:DF。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是
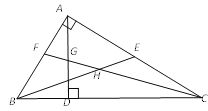
A.①②③④B.①②③C.②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的个数是
①若代数式![]() 有意义,则x的取值范围为x≤1且x≠0.
有意义,则x的取值范围为x≤1且x≠0.
②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.
③若反比例函数![]() (m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
(m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y=x2中偶函数的个数为2个.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“鄂”、“州”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“鄂”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时) | 频数(人数) | 频率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.4 |
2 | 18 | y |
合计 | m | 1 |
(1)统计表中的x= ,y= ;
(2)被调查同学劳动时间的中位数是 时;
(3)请将频数分布直方图补充完整;
(4)求所有被调查同学的平均劳动时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com