Question

【题目】四边形ABCD中，∠B＝∠D＝90°，∠C＝72°，在BC、CD上分别找一点M、N，使△AMN的周长最小时，∠AMN+∠ANM的度数为_______

Answer 1

【答案】144°

【解析】

根据要使△AMN的周长最小，即利用点的对称，让三角形的三边在同一直线上，作出A关于BC和CD的对称点A′，A″，即可得出∠AA′M+∠A″=60°，进而得出∠AMN+∠ANM=2（∠AA′M+∠A″）即可得出答案．

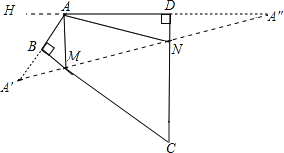
解：作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值．

∵四边形ABCD中，∠B＝∠D＝90°，∠C＝72°

∴∠DAB=108°，

∴∠AA′M+∠A″=72°，

∵∠MA′A=∠MAA′，∠NAD=∠A″，

且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，

∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2（∠AA′M+∠A″）=2×72°=144°，

故填：144°．