
����Ŀ����ͼ����![]() �У�
�У�![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() .����
.����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ������
������![]() ���ٶ����
���ٶ����![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ������
������![]() ���ٶ����
���ٶ����![]() �˶����˶�ʱ����
�˶����˶�ʱ����![]() ��.
��.

��1���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���.
�ij���.
��2�����˶������У��Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() λ���߶�
λ���߶�![]() �Ĵ�ֱƽ�����ϣ������ڣ����
�Ĵ�ֱƽ�����ϣ������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
��3���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
��4���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
���𰸡�(1)CP=8-3t;(2)������;(3)������;(4)������.
��������
��1��ֱ������![]() ������⣻
������⣻
��2�������߶δ�ֱƽ���ߵ����ʿɵ�![]() ���з�����⼴�ɣ�
���з�����⼴�ɣ�
��3������ȫ�������ε����ʿɵ���![]() ����Ϊ
����Ϊ![]() ��
��![]() ��
��
����ֻ��![]() ���з������
���з������![]() ��ֵ���ɣ�
��ֵ���ɣ�
��4����![]() ����Ϊ
����Ϊ![]() ������������
������������![]() ��
��![]() ����
����![]() ��
��![]() ��û�з���������t��ֵ���ʲ�����.
��û�з���������t��ֵ���ʲ�����.
�⣺��1��![]() ��
��
��2������![]() λ���߶�
λ���߶�![]() �Ĵ�ֱƽ�����ϣ�
�Ĵ�ֱƽ�����ϣ�
��![]() ��
��
��![]() ��
��
���![]() .
.
���Դ��ڣ�![]() ��ʱ��
��ʱ��![]() λ���߶�
λ���߶�![]() �Ĵ�ֱƽ������.
�Ĵ�ֱƽ������.
��3����![]() ��
��
��Ϊ![]() ��
��![]() ��
��
����ֻ��![]() ��
��
��![]() �����
�����![]() ��
��
���Դ���![]() .
.
��4����![]() ��
��
��Ϊ![]() ��
��
����������![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
����![]() ������.
������.
�ʴ�Ϊ��(1)CP=8-3t;(2)������;(3)������;(4)������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y��![]() x2��
x2��![]() x��3
x��3![]() ������A��B���㣬��y���ڵ�C����DΪ��C���������߶Գ���ĶԳƵ㣮
������A��B���㣬��y���ڵ�C����DΪ��C���������߶Գ���ĶԳƵ㣮
��1������P����������λ��ֱ��AD�·���һ�����㣬��y������һ����E��x������һ����F������PAD��������ʱ��һ����G�ӵ�P������ÿ��1����λ���ٶ���P��E��F��·���˶�����F�������߶�FB��ÿ��2����λ���ٶ��˶���B���ֹͣ������F�������Ƕ���ʱ������G���˶����������õ�ʱ�����٣�
��2����ͼ�����ڣ�1���ʵ������£�����������ֱ��PB����ƽ�ƣ���P��Bƽ�ƺ�Ķ�Ӧ��ֱ��Ϊ��P'��B'��������y�����Ƿ����һ����Q��ʹ�á�P'QB'Ϊ����ֱ�������Σ������ڣ���ֱ��д�����з���������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
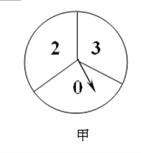
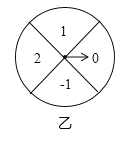
����Ŀ����ͼ����ת�̱��ֳ�3�������ȵ����Σ���ת�̱��ֳ�4�������ȵ����Σ�ÿһ�����ζ�������Ӧ�����֣�ͬʱת������ת�̣���ת��ֹͣ�����ת����ָ����ָ�����ڵ�����Ϊx����ת����ָ����ָ�����ڵ�����Ϊy����ָ��ָ�ڱ߽�����ʱ����תһ�Σ�ֱ��ָ��ָ��һ������Ϊֹ����
��1�������û���״ͼ���б���ķ������г����еȿ��������������㣨x��y�������������ϵĸ��ʣ�
��2��ֱ��д���㣨x��y������������ԭ��ΪԲ�ģ�2Ϊ�뾶��Բ���ĸ���Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ֽƬ![]() �У�
�У�![]() ���۵�ֽƬ��ʹ��
���۵�ֽƬ��ʹ��![]() �պ������߶�
�պ������߶�![]() �ϣ����ۺ۷ֱ���
�ϣ����ۺ۷ֱ���![]() �ཻ�����۵����
�ཻ�����۵����![]() �Ķ�Ӧ��ֱ�Ϊ��
�Ķ�Ӧ��ֱ�Ϊ��![]() ���ۺ۷ֱ���
���ۺ۷ֱ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �����߶�
�����߶�![]() ��ȡֵ��Χ��__________.
��ȡֵ��Χ��__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��1955�꣬ӡ����ѧ�ҿ���Ү����![]() ���о��˶���λ��Ȼ����һ�ֱ任���θ�����λ��
���о��˶���λ��Ȼ����һ�ֱ任���θ�����λ��![]() ����
����![]() ���ĸ������ɴ�С�������г�һ����λ��
���ĸ������ɴ�С�������г�һ����λ��![]() ���ټ�ȥ���ķ�����
���ټ�ȥ���ķ�����![]() ������
������![]() ���ĸ�������С�������У��涨����������������0����0ȥ�����㣬����0001������ʱ��1���㣩���ó���
���ĸ�������С�������У��涨����������������0����0ȥ�����㣬����0001������ʱ��1���㣩���ó���![]() ��Ȼ�������
��Ȼ�������![]() �ظ������任������
�ظ������任������![]() ��������˽�����ȥ������Ү�����֣�����
��������˽�����ȥ������Ү�����֣�����![]() �Ƕ�����λ����ֻҪ�ĸ����ֲ�ȫ��ͬ��������
�Ƕ�����λ����ֻҪ�ĸ����ֲ�ȫ��ͬ��������![]() �������任���ͻ���ֱ任ǰ����ͬ����λ��
�������任���ͻ���ֱ任ǰ����ͬ����λ��![]() ���������Ϊ
���������Ϊ![]() �任�ĺ�.����λ��9631��
�任�ĺ�.����λ��9631��![]() �任�ĺ�Ϊ______.
�任�ĺ�Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��1955�꣬ӡ����ѧ�ҿ���Ү����![]() ���о��˶���λ��Ȼ����һ�ֱ任���θ�����λ��
���о��˶���λ��Ȼ����һ�ֱ任���θ�����λ��![]() ����
����![]() ���ĸ������ɴ�С�������г�һ����λ��
���ĸ������ɴ�С�������г�һ����λ��![]() ���ټ�ȥ���ķ�����
���ټ�ȥ���ķ�����![]() ������
������![]() ���ĸ�������С�������У��涨����������������0����0ȥ�����㣬����0001������ʱ��1���㣩���ó���
���ĸ�������С�������У��涨����������������0����0ȥ�����㣬����0001������ʱ��1���㣩���ó���![]() ��Ȼ�������
��Ȼ�������![]() �ظ������任������
�ظ������任������![]() ��������˽�����ȥ������Ү�����֣�����
��������˽�����ȥ������Ү�����֣�����![]() �Ƕ�����λ����ֻҪ�ĸ����ֲ�ȫ��ͬ��������
�Ƕ�����λ����ֻҪ�ĸ����ֲ�ȫ��ͬ��������![]() �������任���ͻ���ֱ任ǰ����ͬ����λ��
�������任���ͻ���ֱ任ǰ����ͬ����λ��![]() ���������Ϊ
���������Ϊ![]() �任�ĺ�.����λ��9631��
�任�ĺ�.����λ��9631��![]() �任�ĺ�Ϊ______.
�任�ĺ�Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
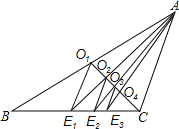
����Ŀ����ͼ����֪CO1����ABC�����ߣ�����O1��O1E1��AC��BC�ڵ�E1������AE1��CO1�ڵ�O2������O2��O2E2��AC��BC�ڵ�E2������AE2��CO1�ڵ�O3������O3��O3E3��AC��BC�ڵ�E3��������˼������������εõ���O4��O5������On�͵�E4��E5������En����OnEn=����AC�����ú�n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��4�£������г�2019���������������Ѿ�˳��������������ʦ����ͬŬ���£�ȡ������ʷ�Եĺóɼ�������С��Ϊ�˽����������������������Գɼ����������ȡ��������ķ��������꼶�������������������ͬѧ���忼�ɼ��������������������������ֳ���5��С�飬�����忼�ɼ��ƶ�������Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ
�����ɼ�Ƶ���ֲ���
��� | �ɼ���x�֣� | Ƶ�� | Ƶ�� |
A | 35��x��38 | 1 | |
B | 38��x��41 | 0.05 | |
C | 41��x��44 | ||
D | 44��x��47 | 6 | |
E | 47��x��50 |
��1������ο����У����������� ����ѧ�������벹ȫƵ���ֲ�ֱ��ͼ��
��2���������ѧ���У���30��������50�֣��������г�2019��ȫ�꼶��1100����ѧ��������Ƹ��꼶�忼�ɼ����ֵ�������Լ�ж�������
��3����������������ȡ�õĻԻͳɼ��ó�����ѧ��ѧ�������Ĵ�����Ϊ�˵�������ѧ�����������ԣ������꼶������1��������������ÿ���Ƽ�һ�˲�����С�����ڵİ༶��ܺͳ������˾��뱨��������Ϊ�˹�ƽѡ�Σ���������С��ͳ�������˽�10�ε������ɼ�����λ����/�֣������£�
��ܳɼ�����/�֣� | 170 | 175 | 180 | 190 | 195 | |||||
���� | l | 1 | 3 | 2 | 3 | |||||
�����ɼ�����/�֣� | 165 | 180 | 190 | 195 | 200 | |||||
���� | 2 | 2 | 3 | 2 | 1 | |||||
�����10�γɼ�����λ������ ��������10�γɼ����������� ��������ͨ��������λͬѧ��ƽ���ɼ��ͷ���������ѡһ��ͬѧ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ߣ�1����ͬѧΪ�˽�2017��ijС����ͥ�¾���ˮ�������������˸�С���IJ��ּ�ͥ�������������ݽ�����������.�����������⣺
�¾���ˮ�� | Ƶ���������� | �ٷֱ� |
| 6 |
|
|
| |
| 16 |
|
| 10 |
|
| 4 | |
| 2 |
|

��1���뽫����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
��2�����С���¾���ˮ��������![]() �ļ�ͥռ�������ͥ�����İٷֱȣ�
�ļ�ͥռ�������ͥ�����İٷֱȣ�
��3������С����1000����ͥ�����ݵ������ݹ��Ƹ�С���¾���ˮ������![]() �ļ�ͥ��.
�ļ�ͥ��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com