
【题目】如图①,抛物线y=![]() x2﹣
x2﹣![]() x﹣3
x﹣3![]() 交轴于A、B两点,交y轴于点C,点D为点C关于抛物线对称轴的对称点.
交轴于A、B两点,交y轴于点C,点D为点C关于抛物线对称轴的对称点.
(1)若点P是抛物线上位于直线AD下方的一个动点,在y轴上有一动点E,x轴上有一动点F,当△PAD的面积最大时,一动点G从点P出发以每秒1个单位的速度沿P→E→F的路径运动到点F,再沿线段FB以每秒2个单位的速度运动到B点后停止,当点F的坐标是多少时,动点G的运动过程中所用的时间最少?
(2)如图②,在(1)问的条件下,将抛物线沿直线PB进行平移,点P、B平移后的对应点分别记为点P'、B',请问在y轴上是否存在一动点Q,使得△P'QB'为等腰直角三角形?若存在,请直接写出所有符合条件的Q点坐标;若不存在,请说明理由.

【答案】(1)点为F(![]() ,0)时,t最小
,0)时,t最小![]() ;(2)存在,点Q的坐标为:(0,﹣
;(2)存在,点Q的坐标为:(0,﹣![]() )或(0,﹣
)或(0,﹣![]() )或(0,
)或(0,![]() )或(0,﹣
)或(0,﹣![]() )
)
【解析】
(1)由题可求出点A、B、C、D,的坐标,点A、D的坐标代入一次函数表达式可得:直线AD的表达式,过点作y轴的平行线交AD于点S,设点P(x,![]() x2﹣
x2﹣![]() x﹣3
x﹣3![]() ),点S(x,﹣
),点S(x,﹣![]() x﹣
x﹣![]() ),可得S△PAD=
),可得S△PAD=![]() SP×(xD﹣xA)=2
SP×(xD﹣xA)=2![]() (﹣
(﹣![]() x﹣
x﹣![]() ﹣
﹣![]() x2+
x2+![]() x+3),由此可得点P的坐标,作点P关于y轴的对称点P′,过点B作与x轴负方向夹角为30°的直线BH,过点P′作PH⊥BH交于点H,P′H于y轴、x轴分别交于点E、F,则此时t最小,然后求出直线BH的表达式和直线P′H的表达式联立求解,从而可得答案;
x+3),由此可得点P的坐标,作点P关于y轴的对称点P′,过点B作与x轴负方向夹角为30°的直线BH,过点P′作PH⊥BH交于点H,P′H于y轴、x轴分别交于点E、F,则此时t最小,然后求出直线BH的表达式和直线P′H的表达式联立求解,从而可得答案;
(2)先求出直线PB的表达式,设:点P′、B′的坐标分别为:(m,![]() m﹣6
m﹣6![]() ),(m+3
),(m+3![]() ,
,![]() m﹣
m﹣![]()
![]() ),分:①当∠B′QP′为直角时,②当∠QB′P′为直角时,③当∠QP′B′为直角时,三种情况讨论即可.
),分:①当∠B′QP′为直角时,②当∠QB′P′为直角时,③当∠QP′B′为直角时,三种情况讨论即可.
(1)y=![]() x2﹣
x2﹣![]() x﹣3
x﹣3![]() ,令y=0,则x=4
,令y=0,则x=4![]() 或﹣
或﹣![]() ,
,
故点A、B的坐标分别为(﹣![]() ,0)、(4
,0)、(4![]() ,0),
,0),
点C(0,﹣3![]() )、点D(3
)、点D(3![]() ,﹣3
,﹣3![]() ),
),
将点A、D的坐标代入一次函数表达式:y=kx+b并解得:
直线AD的表达式为:y=﹣![]() x﹣
x﹣![]() ,
,
过点作y轴的平行线交AD于点S,
设点P(x,![]() x2﹣
x2﹣![]() x﹣3
x﹣3![]() ),点S(x,﹣
),点S(x,﹣![]() x﹣
x﹣![]() )
)
S△PAD=![]() SP×(xD﹣xA)=2
SP×(xD﹣xA)=2![]() (﹣
(﹣![]() x﹣
x﹣![]() ﹣
﹣![]() x2+
x2+![]() x+3
x+3![]() )=﹣
)=﹣![]() x2+3
x2+3![]() x+
x+![]() ,
,
∵﹣![]() <0,
<0,
∴S△PAD有最大值,当x=﹣![]() =
=![]() 时,函数取得最大值,
时,函数取得最大值,
此时点P(![]() ,﹣
,﹣![]() );
);
作点P关于y轴的对称点P′(﹣![]() ,﹣
,﹣![]() ),
),
过点B作与x轴负方向夹角为30°的直线BH,
过点P′作PH⊥BH交于点H,P′H于y轴、x轴分别交于点E、F,则此时t最小,

∵直线BH与x轴负方向夹角为30°,则FH=![]() BF,
BF,
t=PE+EF+![]() FB=P′E+EF+FH=P′H,
FB=P′E+EF+FH=P′H,
设:直线BH的表达式为:y=﹣![]() x+s,
x+s,
将点B的坐标代入上式并解得:
直线BH的表达式为:y=﹣![]() x+4…①,
x+4…①,
同理可得直线P′H的表达式为:y=![]() x+3﹣
x+3﹣![]() …②,
…②,
则点F(![]() ﹣
﹣![]() ,0),
,0),
则直线P′H的倾斜角为60°,
联立①②并解得:x=![]() ,y=
,y=![]() ,
,
即点H(![]() ,
,![]() )
)
t=P′H=2(xH﹣xP′)=![]() ;
;
故点为F(![]() ,0)时,t最小(
,0)时,t最小(![]() );
);
(2)存在,理由:
同理可得直线PB的表达式为:y=![]() x﹣6
x﹣6![]() ,
,
则tan∠GB′P′=![]() =tanα,则cosα=
=tanα,则cosα=![]() ,sinα=
,sinα=![]() ,
,
P′B′=PB=![]() ,则点B′在点P′右侧的距离为:PBcos∠α=3
,则点B′在点P′右侧的距离为:PBcos∠α=3![]() ,
,
同理点B′在点P′上方的距离为:![]() ,
,
则设:点P′、B′的坐标分别为:(m,![]() m﹣6
m﹣6![]() ),(m+3
),(m+3![]() ,
,![]() m﹣
m﹣![]()
![]() ),
),
①当∠B′QP′为直角时,如图(左侧图),

过点B′作B′G⊥y轴于点G,
∵∠B′QG+∠P′OH=90°,∠B′QG+∠GB′Q=90°,∴∠GB′Q=∠P′OH,
∠B′GQ=∠QHP′=90°,QP′=QB′,
∴△B′GQ≌△QHP′(AAS),则B′G=OH,GQ=P′H,
即:![]() m﹣
m﹣![]() ﹣n=m,m+3
﹣n=m,m+3![]() =n﹣
=n﹣![]() m+6
m+6![]() ,
,
解得:m=![]() ,n=﹣
,n=﹣![]() ;
;
同理当直线向下平移时:n=﹣![]() ;
;
②当∠QB′P′为直角时,
同理可得:m+3![]() ﹣m=n﹣
﹣m=n﹣![]() m+
m+![]() ,
,![]() m﹣
m﹣![]() ﹣
﹣![]() m+6
m+6![]() =m+3
=m+3![]() ,
,
解得:m=![]() ,n=
,n=![]() ,
,
同理当直线向下平移时:n=﹣![]() ;
;
③当∠QP′B′为直角时,
经验证同②重复,解得n=![]() ;
;
综上,点Q的坐标为:(0,﹣![]() )或(0,﹣
)或(0,﹣![]() )或(0,
)或(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
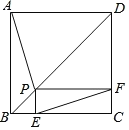
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②△APD一定是等腰三角形;③AP⊥EF;④![]() PD=EF.其中正确结论的番号是( )
PD=EF.其中正确结论的番号是( )
A.①③④B.①②③C.①③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则经过6小时可到达乙地.
(1)甲、乙两地相距多少千米?
(2)如果汽车把速度提高到 v(千米/时),那么从甲地到乙地所用时间 t(小时)将怎样变化?
(3)写出 t与 v之间的函数关系式;
(4)因某种原因,这辆汽车需在5小时内从甲地到达乙地,则此时汽车的平均速度至少应是多少?
(5)已知汽车的平均速度最大可达80千米/时,那么它从甲地到乙地最快需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y1=﹣![]() x2+bx+c的图象与x轴、y轴分别交于点A(﹣1,0)和点B(0,2),图象的对称轴交x轴于点C,一次函数y2=mx+n的图象经过点B、C.
x2+bx+c的图象与x轴、y轴分别交于点A(﹣1,0)和点B(0,2),图象的对称轴交x轴于点C,一次函数y2=mx+n的图象经过点B、C.
(1)求二次函数的解析式y1和一次函数的解析式y2;
(2)点P在x轴下方的二次函数图象上,且S△ACP=33,求点P的坐标;
(3)结合图象,求当x取什么范围的值时,有y1≤y2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一个基本的几何定理,早在我国西汉吋期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫“整数直角三角形”;这三个整数叫做一组“勾股数”,如:3,4,5;5,12,13;7,24,25;8,15,17;9,40,41等等都是勾股数.
(1)小李在研究勾股数时发现,某些整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差.如3,4,5中,5=22+12,3=22﹣12;5,12,13中,13=32+22,5=32﹣22;请证明:m,n为正整数,且m>n,若有一个直角三角形斜边长为m2+n2,有一条直角长为m2﹣n2,则该直角三角形一定为“整数直角三角形”;
(2)有一个直角三角形两直角边长分别为![]() 和
和![]() ,斜边长4
,斜边长4![]() ,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
(3)若c1=a12+b12,c2=a22+b22,其中,a1、a2、b1、b2均为正整数.证明:存在一个整数直角三角形,其斜边长为c1c2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个图案都由若干个“●”组成,其中第①个图案中有7个“●”,第②个图案中有13个“●”,…,则第⑨个图案中“●”的个数为( )

A.87B.91C.103D.111
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF.其中正确的结论有( )
S△ABF.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动;同时动点
运动;同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动,运动时间是
运动,运动时间是![]() 秒.
秒.

(1)用含![]() 的代数式表示
的代数式表示![]() 的长度.
的长度.
(2)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 位于线段
位于线段![]() 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(4)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com