
����Ŀ�����ɶ�����һ�������ļ��ζ����������ҹ������������顶�����㾭�����С������������塱�ļ��أ����һ��ֱ�����������߳�������������������ֱ�������νС�����ֱ�������Ρ�����������������һ�顰�����������磺3��4��5��5��12��13��7��24��25��8��15��17��9��40��41�ȵȶ��ǹ�������
��1��С�����о�������ʱ���֣�ijЩ����ֱ�������ε�б����д������������ƽ���ͣ���һ��ֱ�DZ���д��������������ƽ�����3��4��5�У�5��22+12��3��22��12��5��12��13�У�13��32+22��5��32��22����֤����m��nΪ����������m��n������һ��ֱ��������б�߳�Ϊm2+n2����һ��ֱ�dz�Ϊm2��n2�����ֱ��������һ��Ϊ������ֱ�������Ρ���
��2����һ��ֱ����������ֱ�DZ߳��ֱ�Ϊ![]() ��
��![]() ��б�߳�4
��б�߳�4![]() ����a��b��Ϊ���������ú�b�Ĵ���ʽ��ʾa�������a��b��ֵ��
����a��b��Ϊ���������ú�b�Ĵ���ʽ��ʾa�������a��b��ֵ��
��3����c1��a12+b12��c2��a22+b22�����У�a1��a2��b1��b2��Ϊ��������֤��������һ������ֱ�������Σ���б�߳�Ϊc1c2��
���𰸡���1������������2��![]() ��a��31��b��4����3��������
��a��31��b��4����3��������
��������
��1�����ݹ��ɶ��������ã�m2+n2��2����m2��n2��2�������һ��ֱ�DZ߳�Ϊ2mn����Ϊm��nΪ������������2mnҲΪ�����������ɵ�֤��
��2�����ȸ��ݹ��ɶ������![]() ����
����![]() �Ĵ���ʽ���ٸ��ݱ�����������ڵ���0���������
�Ĵ���ʽ���ٸ��ݱ�����������ڵ���0���������![]() ��
��![]() �ķ�Χ����
�ķ�Χ����![]() ��
��![]() ��Ϊ����������b�Ŀ���ֵ��1��2��3��4�ֱ���룬������÷���������������
��Ϊ����������b�Ŀ���ֵ��1��2��3��4�ֱ���룬������÷���������������![]() ��
��![]() ��
��
��3���۲췢�֣���a1��b1��1��a2��b2��2ʱ��c1c2��5��5��25����![]() ���ʴ��ڣ�
���ʴ��ڣ�
��1��֤����
�ߣ�m2+n2��2����m2��n2��2��
����m2+n2+m2��n2����m2+n2��m2+n2����
��2m22n2��
����2mn��2��
�ࣨ2mn��2+��m2��n2��2����m2+n2��2��
��m��n����������m��n��
��2mn��m2��n2��m2+n2����������
���ֱ��������һ��Ϊ������ֱ�������Ρ���
��2���ɹ��ɶ����ã�
7a��7+��150��30b����16��15��
��![]() ��
��
�������֪��7a��7��0��150��30b��0��
��a��1��0��b��5��
��a��b����������
��b�Ŀ���ֵΪ��1��2��3��4��
��b��1ʱ��![]() ����������������b��1���������⣻
����������������b��1���������⣻
��b��2ʱ��![]() ����������������b��2���������⣻
����������������b��2���������⣻
��b��3ʱ��![]() ����������������b��3���������⣻
����������������b��3���������⣻
��b��4ʱ��![]() ��������������ʱ
��������������ʱ![]()
![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��b��4�������⣬
��![]() ��a��31��b��4��
��a��31��b��4��
��3��֤�����۲췢�֣���a1��b1��1��a2��b2��2ʱ��c1c2��5��5��25��
152+202��225+400��625��252��625��
��152+202��252��
�����һ������ֱ�������Σ���б�߳�Ϊc1c2��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������Ϊ�������赸��ͳһ�ӷ��͵��ߣ������� 10 ��ij��Ʒ�Ƶ��赸Ь��ÿ˫�赸Ь�� x��x��2�����赸�ȣ����赸�Ӷ�Աʹ�ã����������� A��B ���ҳ��ж�������Ʒ�Ƶ��赸Ь���赸�ȳ��ۣ���ÿ˫�赸Ь�ı�۾�Ϊ 30 Ԫ��ÿ���赸�ȵı��Ϊ 3 Ԫ��Ŀǰ���ҳ���ͬʱ�����������
A ���У�������Ʒ������ۣ�����۵� 90%�����ۣ�
B ���У���һ˫�赸Ь�� 2 ���赸�ȣ�
���� A ���й����赸Ь���赸�ȵķ���Ϊ![]() ��Ԫ������ B ���й����赸Ь���赸�ȵķ���Ϊ
��Ԫ������ B ���й����赸Ь���赸�ȵķ���Ϊ ![]() ��Ԫ���������������⣺
��Ԫ���������������⣺
��1���ֱ�д�� ![]() ��
��![]() �� x ֮��Ĺ�ϵʽ��
�� x ֮��Ĺ�ϵʽ��
��2�����û����ֻ��һ�ҳ��й�������Ϊ���ļҳ��й�������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
С����ѧϰ�˶��θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ������3��2![]() ��(1��
��(1��![]() )2.����˼����С������������̽����
)2.����˼����С������������̽����
��a��b![]() ��(m��n
��(m��n![]() )2(����a��b��m��n��������)������a��b
)2(����a��b��m��n��������)������a��b![]() ��m2��2n2��2mn
��m2��2n2��2mn![]() .
.
��a��m2��2n2��b��2mn.����С�����ҵ���һ�ְѲ�������a��b![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
�������С���ķ���̽��������������⣺
(1)��a��b��m��n��Ϊ������ʱ����a��b![]() ��(m��n
��(m��n![]() )2���ú�m��n��ʽ�ӷֱ��ʾa��b����a��__________��b��__________��
)2���ú�m��n��ʽ�ӷֱ��ʾa��b����a��__________��b��__________��
(2)������̽���Ľ��ۣ���һ��������a��b��m��n��գ�________��________![]() ��(________��________
��(________��________![]() )2��
)2��
(3)��a��4![]() ��(m��n
��(m��n![]() )2����a��m��n��Ϊ����������a��ֵ��
)2����a��m��n��Ϊ����������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɱ߳�Ϊ1��С��������ɵ�![]() ����ֱ��
����ֱ��![]() ��һ�������ߣ���
��һ�������ߣ���![]() ��
��![]() �ڸ���ϣ�
�ڸ���ϣ�![]() ���������㶼�ڸ�㣨�����ߵĽ��㣩��.
���������㶼�ڸ�㣨�����ߵĽ��㣩��.

��1������![]() ����ֱ��
����ֱ��![]() �ԳƵ�
�ԳƵ�![]() ��
��
��2����ֱ��![]() �ϻ�����
�ϻ�����![]() ��ʹ�ı���
��ʹ�ı���![]() ���ܳ���С��
���ܳ���С��
��3�������![]() ����������
�����У�����![]() �͵�
�͵�![]() �ľ�����ȵĸ����_________��.
�ľ�����ȵĸ����_________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ���Σ�FΪ�Խ���BD��һ�㣬��E��BA�ӳ����ϣ�
��1����ͼ������FΪ���ζԽ���AC��BD�Ľ��㣬��E��BA�ӳ�������BE��AC������DE��M��DE���е㣬����BM��FM��AD��6��FM��![]() �����߶�AE�ij���
�����߶�AE�ij���
��2����ͼ��������F��FE��BD��AD�ڵ�H����BA�ӳ����ڵ�E������AF����FD��FEʱ����֤��HA+AB��![]() AF��
AF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y��![]() x2��
x2��![]() x��3
x��3![]() ������A��B���㣬��y���ڵ�C����DΪ��C���������߶Գ���ĶԳƵ㣮
������A��B���㣬��y���ڵ�C����DΪ��C���������߶Գ���ĶԳƵ㣮
��1������P����������λ��ֱ��AD�·���һ�����㣬��y������һ����E��x������һ����F������PAD��������ʱ��һ����G�ӵ�P������ÿ��1����λ���ٶ���P��E��F��·���˶�����F�������߶�FB��ÿ��2����λ���ٶ��˶���B���ֹͣ������F�������Ƕ���ʱ������G���˶����������õ�ʱ�����٣�
��2����ͼ�����ڣ�1���ʵ������£�����������ֱ��PB����ƽ�ƣ���P��Bƽ�ƺ�Ķ�Ӧ��ֱ��Ϊ��P'��B'��������y�����Ƿ����һ����Q��ʹ�á�P'QB'Ϊ����ֱ�������Σ������ڣ���ֱ��д�����з���������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O�ֱ�����ABC��������AB��BC��CA�ڵ�D��E��F��S��ABC=10cm2��C��ABC=10cm�ҡ�C=60������
��1����O�İ뾶r��
��2������OEF��������������������
��3������OEF���ܳ��������������
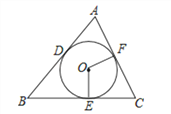
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�P�ǶԽ���AC�ϵ�һ�㣬��E��BC���ӳ����ϣ���PE=PB��
��1����PC=CEʱ������CDP�Ķ�����
��2�����õ�ʽ��ʾ�߶�PB��BC��CE֮���������ϵ����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��1955�꣬ӡ����ѧ�ҿ���Ү����![]() ���о��˶���λ��Ȼ����һ�ֱ任���θ�����λ��
���о��˶���λ��Ȼ����һ�ֱ任���θ�����λ��![]() ����
����![]() ���ĸ������ɴ�С�������г�һ����λ��
���ĸ������ɴ�С�������г�һ����λ��![]() ���ټ�ȥ���ķ�����
���ټ�ȥ���ķ�����![]() ������
������![]() ���ĸ�������С�������У��涨����������������0����0ȥ�����㣬����0001������ʱ��1���㣩���ó���
���ĸ�������С�������У��涨����������������0����0ȥ�����㣬����0001������ʱ��1���㣩���ó���![]() ��Ȼ�������
��Ȼ�������![]() �ظ������任������
�ظ������任������![]() ��������˽�����ȥ������Ү�����֣�����
��������˽�����ȥ������Ү�����֣�����![]() �Ƕ�����λ����ֻҪ�ĸ����ֲ�ȫ��ͬ��������
�Ƕ�����λ����ֻҪ�ĸ����ֲ�ȫ��ͬ��������![]() �������任���ͻ���ֱ任ǰ����ͬ����λ��
�������任���ͻ���ֱ任ǰ����ͬ����λ��![]() ���������Ϊ
���������Ϊ![]() �任�ĺ�.����λ��9631��
�任�ĺ�.����λ��9631��![]() �任�ĺ�Ϊ______.
�任�ĺ�Ϊ______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com