
【题目】阅读材料:
小明在学习了二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n均为正整数),则有a+b
)2(其中a,b,m,n均为正整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分形如a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a=__________,b=__________;
)2,用含m,n的式子分别表示a,b,得a=__________,b=__________;
(2)利用所探索的结论,找一组正整数a,b,m,n填空:________+________![]() =(________+________
=(________+________![]() )2;
)2;
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n均为正整数,求a的值.
)2,且a,m,n均为正整数,求a的值.
【答案】(1)m2+3n2,2mn;(2) 4,2,1,1(答案不唯一);(3) 13
【解析】(1)根据完全平方公式运算法则,即可得出a、b的表达式;
(2)首先确定好m、n的正整数值,然后根据(1)的结论即可求出a、b的值;
(3)根据题意,4=2mn,首先确定m、n的值,通过分析m=2,n=1或者m=1,n=2,然后即可确定好a的值.
解:(1)∵a+b![]() =
=![]() ,
,
∴a+b![]() =m2+3n2+2mn
=m2+3n2+2mn![]() ,
,
∴a=m2+3n2,b=2mn.
故答案为:m2+3n2,2mn.
(2)设m=1,n=1,
∴a=m2+3n2=4,b=2mn=2.
故答案为4、2、1、1.
(3)由题意,得:
a=m2+3n2,b=2mn
∵4=2mn,且m、n为正整数,
∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.
“点睛”本题主要考查二次根式的混合运算,完全平方公式,解题的关键在于熟练运算完全平方公式和二次根式的运算法则.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人 | 测试成绩 | ||
题目 | 甲 | 乙 | 丙 |
文化课知识 | 74 | 87 | 69 |
面试 | 58 | 74 | 70 |
平时表现 | 87 | 43 | 65 |
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)从图中可知,小明家离体育馆 米,父子俩在出发后 分钟相遇.
(2)求出父亲与小明相遇时距离体育馆还有多远?
(3)小明能否在比赛开始之前赶回体育馆?

查看答案和解析>>
科目:初中数学 来源: 题型:
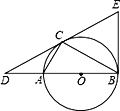
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
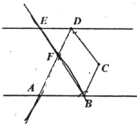
【题目】如图,已知![]() 为两条相互平行的直线
为两条相互平行的直线![]() ,
,![]() 之间一点,
之间一点,![]() 和
和![]() 的角平分线相交于
的角平分线相交于![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)连结![]() 当
当![]() 且
且![]() 时,求
时,求![]() 的度数;
的度数;
(3)若![]() 时,将线段
时,将线段![]() 沿直线
沿直线 ![]() 方向平移,记平移后的线段为
方向平移,记平移后的线段为![]() (
(![]() ,
,![]() 分别对应
分别对应![]() 、
、![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的度数_______.
的度数_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则经过6小时可到达乙地.
(1)甲、乙两地相距多少千米?
(2)如果汽车把速度提高到 v(千米/时),那么从甲地到乙地所用时间 t(小时)将怎样变化?
(3)写出 t与 v之间的函数关系式;
(4)因某种原因,这辆汽车需在5小时内从甲地到达乙地,则此时汽车的平均速度至少应是多少?
(5)已知汽车的平均速度最大可达80千米/时,那么它从甲地到乙地最快需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,矩形内一动点P使得S△PAD=![]() S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.
S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一个基本的几何定理,早在我国西汉吋期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫“整数直角三角形”;这三个整数叫做一组“勾股数”,如:3,4,5;5,12,13;7,24,25;8,15,17;9,40,41等等都是勾股数.
(1)小李在研究勾股数时发现,某些整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差.如3,4,5中,5=22+12,3=22﹣12;5,12,13中,13=32+22,5=32﹣22;请证明:m,n为正整数,且m>n,若有一个直角三角形斜边长为m2+n2,有一条直角长为m2﹣n2,则该直角三角形一定为“整数直角三角形”;
(2)有一个直角三角形两直角边长分别为![]() 和
和![]() ,斜边长4
,斜边长4![]() ,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
(3)若c1=a12+b12,c2=a22+b22,其中,a1、a2、b1、b2均为正整数.证明:存在一个整数直角三角形,其斜边长为c1c2.
查看答案和解析>>
科目:初中数学 来源: 题型:
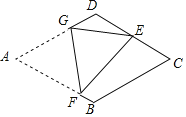
【题目】如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com