
����Ŀ�������й��������������𡢼��ô���Ĺ����������۷���������2014��3��25��-27�������������ݾ��С�С�����������ݿ�����������ʱ��������Ʊ���ڼ����ʱ�������ʼ����25���ӣ������������лؼ�ȡƱ��ͬʱ�������״Ӽ�����������г�����3�����ٶȸ�����Ʊ��������;��������������С���������������г��ϻ������ݣ���ͼ���߶�AB��OB�ֱ��ʾ����������Ʊ��ȡƱ�����У��������ݵ�·��S���ף�������ʱ��t�����ӣ�֮���ͼ���ͼ�����������⣨���������г��Ͳ��е��ٶ�ʼ�ձ��ֲ��䣩��
��1����ͼ�п�֪��С������������ �ף��������ڳ����� ����������
��2�����������С������ʱ���������ݻ��ж�Զ��
��3��С���ܷ��ڱ�����ʼ֮ǰ�ϻ������ݣ�

���𰸡���1��3600��15��(2) 900�� (3) С�����ڱ�����ʼ֮ǰ�ϻ������ݣ�
����������������1���۲�ͼ��õ�С��������������3600����С���������ص�ʱ����15��������õ��������ڳ�����15����������
��2����С�����ٶ�Ϊx��/�������������ٶ�Ϊ3x��/�������ø������ڳ�����15���������õ�15x+3x15=3600�����x=60��/����������С������ʱ���������ݻ���15x=900����
��3���ɣ�2���õ���B�㵽O����ٶ�Ϊ3x=180��/�������B�㵽O�������ʱ��=![]() =5���֣����õ�С��ȡƱ�ص�����������15+5=20������С��25���������ж�С�����ڱ�����ʼ֮ǰ�ϻ������ݣ�
=5���֣����õ�С��ȡƱ�ص�����������15+5=20������С��25���������ж�С�����ڱ�����ʼ֮ǰ�ϻ������ݣ�
�������1����O����A�����3600������С��������������3600�ף�
�ߴӵ�O�㵽��B����15�������ุ�����ڳ�����15����������
��2����С�����ٶ�Ϊx��/�������������ٶ�Ϊ3x��/���������������
15x+3x15=3600��
�����x=60��/������15x=15��60=900���ף�
��������С������ʱ���������ݻ���900����
��3���ߴ�B�㵽O����ٶ�Ϊ3x=180��/�������B�㵽O�������ʱ��=![]() =5���֣�����С���������ݵ���B����15��������С���ӵ�O����B���ٴӵ�B����O��15��+5��=20�֣�
=5���֣�����С���������ݵ���B����15��������С���ӵ�O����B���ٴӵ�B����O��15��+5��=20�֣�
��С���������ݳ���ȡƱʱ���������ʼ����25��������С�����ڱ�����ʼ֮ǰ�ϻ������ݣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���P�����ɵ�P��2��3��������ƽ��3����λ��������ƽ��2����λ�õ��ģ����P���������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=x2��2x+c�Ķ���A��ֱ��l��y=x��5�ϣ�
��1���������߶���A�����ꣻ
��2������������y�ύ�ڵ�B����x�ύ�ڵ�C��D��C����D�����ࣩ�����жϡ�ABD����״��
��3����ֱ��l���Ƿ����һ��P��ʹ�Ե�P��A��B��DΪ������ı�����ƽ���ı��Σ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ������Ϊ��ǿ��Ѵ������������ijˮ���ӽ��мӹ̣���ӵĺ����������ABCD����ͼ��ʾ����֪ӭˮ����AB�ij�Ϊ16�ף���B=60�㣬��ˮ����CD�ij�Ϊ ![]() �ף��ӹ̺��ӵĺ�����Ϊ����ABED��CE�ij�Ϊ8�ף�
�ף��ӹ̺��ӵĺ�����Ϊ����ABED��CE�ij�Ϊ8�ף�
��1����֪��ӹ̵Ĵ�ӳ�Ϊ150�ף�����Ҫ����ʯ�����������ף�
��2����ӹ̺�Ĵ�ӱ�ˮ����DE���¶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��һ�ų�����ֽƬ�ֱ�����EP,FP���ۣ�ʹB����B�䣬C����C�䣮
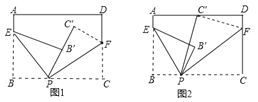
��1������P,B��,C����ͬһֱ����(ͼ1�����������ۺ۵ļнǡ�EPF�Ķ�����
��2������P,B��,C������ͬһֱ����(ͼ2�����ҡ�B��PC��=10�������EPF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������� ![]() ��ͼ��xȡ1��2��3������nʱ����Ӧ�ڷ�����ͼ���ϵĵ�ֱ�ΪM1 �� M2 �� M3����Mn �� ��
��ͼ��xȡ1��2��3������nʱ����Ӧ�ڷ�����ͼ���ϵĵ�ֱ�ΪM1 �� M2 �� M3����Mn �� �� ![]() = ��
= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������һ��ͼ�Σ�ͨ����ͬ�ķ�������ͼ�ε�������Եõ�һ����ѧ��ʽ��
���磺��ͼ1�ɵõ�(a+b)=a+2ab+b��



ͼ1 ͼ2 ͼ3
��1��д����ͼ2����ʾ����ѧ��ʽ��_____________________��д����ͼ3����ʾ����ѧ��ʽ��_____________________��
��2�������������ۣ�����������⣺��֪a+b+c=11��bc+ac+ab=38����a+b+c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��һ�������������˾ӵ���̬������ij��������ס��ҡ���������������ׯ����֪�ס��ұ��������ļ۸�֮��Ϊ2��2��3��������ÿ��200Ԫ���ּƻ���210000Ԫ�ʽ𣬹�������������1000����
��1�����ҡ���������ÿ�ø�����Ԫ��
��2��������������Ŀ�������������2����ǡ������ƻ��ʽ��������������ܹ�����ٿã�
��3������������10120Ԫ�Ĺ�����ڹ����ܿ��������ǰ���£�������������Թ�����ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD�У�G��CD��һ�㣬�ӳ�BC��E��ʹCE=CG������BG���ӳ���DE��F��
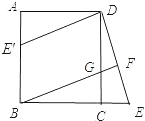
��1����֤����BCG�ա�DCE��
��2������DCE�Ƶ�D˳ʱ����ת90���õ���DAE�����ж��ı���E��BGD��ʲô�����ı��Σ���˵��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com