
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
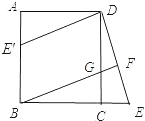
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由。
【答案】(1)答案见解析;(2)答案见解析
【解析】试题分析:(1)由正方形ABCD,得BC=CD,∠BCD=∠DCE=90°,又CG=CE,所以△BCG≌△DCE(SAS).
(2)由(1)得BG=DE,又由旋转的性质知AE′=CE=CG,所以BE′=DG,从而证得四边形E′BGD为平行四边形.
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
又∵CG=CE,
∴△BCG≌△DCE.
(2)解:四边形E′BGD是平行四边形.理由如下:
∵△DCE绕D顺时针旋转90°得到△DAE′,
∴CE=AE′.
∵CE=CG,
∴CG=AE′.
∵四边形ABCD是正方形,
∴BE′∥DG,AB=CD.
∴AB﹣AE′=CD﹣CG.
即BE′=DG.
∴四边形E′BGD是平行四边形.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)从图中可知,小明家离体育馆 米,父子俩在出发后 分钟相遇.
(2)求出父亲与小明相遇时距离体育馆还有多远?
(3)小明能否在比赛开始之前赶回体育馆?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将点A先向下平移3个单位,再向右平移2个单位后得B(﹣2,5),则A点坐标为( )
A.(﹣4,11)B.(﹣2,6)C.(﹣4,8)D.(﹣6,8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=8cm,AD=6cm,按下列步骤进行裁剪和拼图: 
第一步:如图①,在线段AD上任意取一点E,沿EB,EC剪下一个三角形纸片EBC(余下部分不再使用);
第二步:如图②,沿三角形EBC的中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;
第三步:如图③,将MN左侧纸片绕G点按顺时针方向旋转180°,使线段GB与GE重合,将MN右侧纸片绕H点按逆时针方向旋转180°,使线段HC与HE重合,拼成一个与三角形纸片EBC面积相等的四边形纸片.
(注:裁剪和拼图过程均无缝且不重叠)
则拼成的这个四边形纸片的周长的最小值为cm,最大值为cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数 ![]() (m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E的坐标及相应的平行四边形的面积;若不存在,请说明理由;
(3)若P是抛物线对称轴上使△ACP的周长取得最小值的点,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1 , y1),M2(x2 , y2)两点,试探究 ![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com