
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

【答案】(1)证明过程见解析;(2)8.
【解析】试题分析:(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF, ∵E是ABCD的边CD的中点, ∴DE=CE,
在△ADE和△FCE中,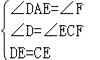 ,∴△ADE≌△FCE(AAS);
,∴△ADE≌△FCE(AAS);
(2)∵ADE≌△FCE, ∴AE=EF=3, ∵AB∥CD, ∴∠AED=∠BAF=90°,
在ABCD中,AD=BC=5, ∴DE=![]() =
=![]() =4, ∴CD=2DE=8
=4, ∴CD=2DE=8


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,现计划用210000元资金,购买这三种树共1000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵树是乙种树的2倍,恰好用完计划资金,求这三种树各能购买多少棵?
(3)若又增加了10120元的购树款,在购买总棵树不变的前提下,求丙种树最多可以购买多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
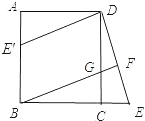
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( ) 
A.M或O或N
B.E或O或C
C.E或O或N
D.M或O或C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:
如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.

小明的思路是:
过点P作PE//AB,

∴∠PAB+∠APE=180°.
∵∠PAB=130°,∴∠APE=50°
∵AB//CD,PE//AB,∴PE//CD,
∴∠PCD+∠CPE=180°.
∵∠PCD=120°,∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
如果AB与CD平行关系不变,动点P在直线AB、CD所夹区域内部运动时,∠PAB,∠PCD的度数会跟着发生变化.
(1)如图3,当动点P运动到直线AC右侧时,请写出∠PAB,∠PCD和∠APC之间的数量关系?并说明理由.

(2)如图4,AQ,CQ分别平分∠PAB,∠PCD,那么∠AQC和角∠APC有怎择的数量关系?

(3)如图5,点P在直线AC的左侧时,AQ,CQ仍然平分∠PAB,∠PCD,请直接写出∠AQC和角∠APC的数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y= ![]() (x>0)的图象与一次函 数y=﹣x+b的图象分别交于A(1,3)、B两点.
(x>0)的图象与一次函 数y=﹣x+b的图象分别交于A(1,3)、B两点.
(1)求m、b的值;
(2)若点M是反比例函数图象上的一动点,直线MC⊥x轴于C,交直线AB于点N,MD⊥y轴于D,NE⊥y轴于E,设四边形MDOC、NEOC的面积分别为S1、S2 , S=S2﹣S1 , 求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com