
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.
例如:由图1可得到(a+b)=a+2ab+b.



图1 图2 图3
(1)写出由图2所表示的数学等式:_____________________;写出由图3所表示的数学等式:_____________________;
(2)利用上述结论,解决下面问题:已知a+b+c=11,bc+ac+ab=38,求a+b+c的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是 ![]() 的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论: ①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④APAD=CQCB.
的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论: ①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④APAD=CQCB.
其中正确的是(写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),y=PC2 , 则y关于x的函数的图象大致为( )
A.
B.
C.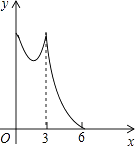
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)从图中可知,小明家离体育馆 米,父子俩在出发后 分钟相遇.
(2)求出父亲与小明相遇时距离体育馆还有多远?
(3)小明能否在比赛开始之前赶回体育馆?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.求证:∠AHF=∠BGF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江海化工厂计划生产甲、乙两种季节性产品,在春季中,甲种产品售价50千元/件,乙种产品售价30千元/件,生产这两种产品需要A、B两种原料,生产甲产品需要A种原料4吨/件,B种原料2吨/件,生产乙产品需要A种原料3吨/件,B种原料1吨/件,每个季节该厂能获得A种原料120吨,B种原料50吨.
(1)如何安排生产,才能恰好使两种原料全部用完?此时总产值是多少万元?
(2)在夏季中甲种产品售价上涨10%,而乙种产品下降10%,并且要求甲种产品比乙种产品多生产25件,问如何安排甲、乙两种产品,使总产值是1375千元,A,B两种原料还剩下多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数 ![]() (m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E的坐标及相应的平行四边形的面积;若不存在,请说明理由;
(3)若P是抛物线对称轴上使△ACP的周长取得最小值的点,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1 , y1),M2(x2 , y2)两点,试探究 ![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com