
【题目】如图,四边形ABCD为矩形,F为对角线BD上一点,点E在BA延长线上.
(1)如图①,若F为矩形对角线AC、BD的交点,点E在BA延长线上且BE=AC,连接DE,M是DE的中点,连接BM,FM若AD=6,FM=![]() ,求线段AE的长;
,求线段AE的长;
(2)如图②,过点F作FE⊥BD交AD于点H,交BA延长线于点E,连接AF,当FD=FE时,求证:HA+AB=![]() AF.
AF.

【答案】(1)3;(2)见解析
【解析】
(1)由矩形的性质可得AC=BD,BF=DF,由中位线定理可得BE=2MF,再由勾股定理可求AB的长,即可求AE的长;
(2)如图②,过点F作FN⊥AF交AB的延长线于点N,由“ASA”可证△EFN≌△DFA,可得∠DAF=∠N,AF=FN,由等腰直角三角形的性质可得AN=![]() ,由“ASA”可证△AHF≌△NBF,可证AH=BN,即可得结论.
,由“ASA”可证△AHF≌△NBF,可证AH=BN,即可得结论.
(1)∵四边形ABCD是矩形
∴AC=BD,BF=DF,
∵M是DE的中点,BF=DF,
∴BE=2MF=![]() ,
,
∵BE=AC,AC=BD
∴BD=![]() ,
,
∴AB=![]() ,
,
∴AE=BE﹣AB=3,
(2)如图②,过点F作FN⊥AF交AB的延长线于点N,

∵EF⊥DF,EA⊥AD,
∴∠E+∠AHE=90°,∠ADF+∠DHF=90°,
∴∠E=∠ADF,
∵∠AFN=∠EFD=90°,
∴∠AFD=∠EFN,且∠E=∠ADF,且EF=DF,
∴△EFN≌△DFA(ASA)
∴∠DAF=∠N,AF=FN,且∠AFN=90°,
∴AN=![]() AF,
AF,
∵∠AFN=∠EFB=90°,
∴∠AFH=∠BFN,且∠DAF=∠N,AF=FN,
∴△AHF≌△NBF(ASA),
∴AH=BN(全等三角形对应边相等),
∵AN=![]() AF,
AF,
∴AB+BN=AB+AH=![]() AF,
AF,


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】学期即将结束,为了表彰优秀,班主任王老师用W元钱购买奖品。若以2支钢笔和3本笔记本为一份奖品,则可买60份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品。设钢笔单价为x元/支,笔记本单价为y元/本。
![]() 请用y的代数式表示x.
请用y的代数式表示x.
![]() 若用这W元钱全部购买笔记本,总共可以买几本?
若用这W元钱全部购买笔记本,总共可以买几本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为两条相互平行的直线
为两条相互平行的直线![]() ,
,![]() 之间一点,
之间一点,![]() 和
和![]() 的角平分线相交于
的角平分线相交于![]() ,
,![]() .
.
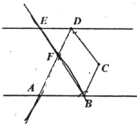

(1)求证:![]() ;
;
(2)连结![]() 当
当![]() 且
且![]() 时,求
时,求![]() 的度数;
的度数;
(3)若![]() 时,将线段
时,将线段![]() 沿直线
沿直线 ![]() 方向平移,记平移后的线段为
方向平移,记平移后的线段为![]() (
(![]() ,
,![]() 分别对应
分别对应![]() 、
、![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的度数_______.
的度数_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,矩形内一动点P使得S△PAD=![]() S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.
S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要做两个形状相同的三角形框架,其中一个三角形框架的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?你选的木料唯一吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一个基本的几何定理,早在我国西汉吋期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫“整数直角三角形”;这三个整数叫做一组“勾股数”,如:3,4,5;5,12,13;7,24,25;8,15,17;9,40,41等等都是勾股数.
(1)小李在研究勾股数时发现,某些整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差.如3,4,5中,5=22+12,3=22﹣12;5,12,13中,13=32+22,5=32﹣22;请证明:m,n为正整数,且m>n,若有一个直角三角形斜边长为m2+n2,有一条直角长为m2﹣n2,则该直角三角形一定为“整数直角三角形”;
(2)有一个直角三角形两直角边长分别为![]() 和
和![]() ,斜边长4
,斜边长4![]() ,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
(3)若c1=a12+b12,c2=a22+b22,其中,a1、a2、b1、b2均为正整数.证明:存在一个整数直角三角形,其斜边长为c1c2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )

A.96B.48C.60D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:

(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com