练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】1955年，印度数学家卡普耶卡（）研究了对四位自然数的一种变换：任给出四位数，用的四个数字由大到小重新排列成一个四位数，再减去它的反序数（即将的四个数字由小到大排列，规定反序后若左边数字有0，则将0去掉运算，比如0001，计算时按1计算），得出数，然后继续对重复上述变换，得数，…，如此进行下去，卡普耶卡发现，无论是多大的四位数，只要四个数字不全相同，最多进行次上述变换，就会出现变换前后相同的四位数，这个数称为变换的核.则四位数9631的变换的核为______.

    【答案】6174

    【解析】

    用9631的四个数字由大到小排列成一个四位数9631．则9631-1369=8262，用8262的四个数字由大到小重新排列成一个四位数8622．则8622-2268=6354，类似地进行上述变换，可知5次变换之后，此时开始停在一个数6174上．

    解：用9631的四个数字由大到小排列成一个四位数9631．则9631-1369=8262，
    用8262的四个数字由大到小重新排列成一个四位数8622．则8622-2268=6354，
    用6354的四个数字由大到小重新排列成一个四位数6543．则6543-3456=3087，
    用3087的四个数字由大到小重新排列成一个四位数8730．则8730-378=8352，
    用8352的四个数字由大到小重新排列成一个四位数8532．则8532-2358=6174，
    用6174的四个数字由大到小重新排列成一个四位数7641．则7641-1467=6174…
    可知7次变换之后，四位数最后都会停在一个确定的数6174上．
    故答案为：6174.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】勾股定理是一个基本的几何定理，早在我国西汉吋期算书《周髀算经》就有“勾三股四弦五”的记载．如果一个直角三角形三边长都是正整数，这样的直角三角形叫“整数直角三角形”；这三个整数叫做一组“勾股数”，如：3，4，5；5，12，13；7，24，25；8，15，17；9，40，41等等都是勾股数．

    （1）小李在研究勾股数时发现，某些整数直角三角形的斜边能写成两个整数的平方和，有一条直角边能写成这两个整数的平方差．如3，4，5中，5＝22+12，3＝22﹣12；5，12，13中，13＝32+22，5＝32﹣22；请证明：m，n为正整数，且m＞n，若有一个直角三角形斜边长为m2+n2，有一条直角长为m2﹣n2，则该直角三角形一定为“整数直角三角形”；

    （2）有一个直角三角形两直角边长分别为和，斜边长4，且a和b均为正整数，用含b的代数式表示a，并求出a和b的值；

    （3）若c1＝a12+b12，c2＝a22+b22，其中，a1、a2、b1、b2均为正整数．证明：存在一个整数直角三角形，其斜边长为c1c2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形纸片ABCD中，AB＝4，∠A＝60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上．则sin∠EFG的值为________．

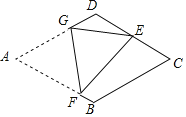
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某校的数学学科实践活动课上，老师布置的任务是对本校七年级学生零花钱使用情况进行随机抽样调查，调查结果分为“A.买零食”、“B.买学习用品”、“C.玩网络游戏”、“D.捐款”四项进行统计，学生将统计结果绘制成了如下两幅不完整的统计图（图1、图2），请根据图中的信息解答下列问题.

    （1）这次调查的学生为______人，图2中，______，______.

    （2）补全图1中的条形统计图.

    （3）在图2的扇形统计图中，表示“C.玩网络游戏”所在扇形的圆心角度数为______度.

    （4）据统计，辽阳市七年级约有学生12000人，那么根据抽样调查的结果，可估计零花钱用于“D.捐款”的学生约有______人.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请认真观察图形，解答下列问题：

    （1）根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；

    （2）由（1），你能得到怎样的等量关系？请用等式表示；

    （3）如果图中的a，b（a＞b）满足a2+b2=53，ab=14，求：①a+b的值；②a4﹣b4的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，为的中点，，.动点从点出发，沿方向以的速度向点运动；同时动点从点出发，沿方向以的速度向点运动，运动时间是秒.

    （1）用含的代数式表示的长度.

    （2）在运动过程中，是否存在某一时刻，使点位于线段的垂直平分线上？若存在，求出的值；若不存在，请说明理由.

    （3）是否存在某一时刻，使？若存在，求出的值；若不存在，请说明理由.

    （4）是否存在某一时刻，使？若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为的正方形四个角上，分别剪去大小相等的等腰直角三角形，当三角形的直角边由小变大时，阴影部分的面积也随之发生变化，它们的变化情况如下：

    三角形的直角边长/

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    阴影部分的面积/

    398

    392

    382

    368

    350

    302

    272

    200

    （1）在这个变化过程中，自变量、因变量各是什么？

    （2）请将上述表格补充完整；

    （3）当等腰直角三角形的直角边长由增加到时，阴影部分的面积是怎样变化的？

    （4）设等腰直角三角形的直角边长为，图中阴影部分的面积为，写出与的关系式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】端午节是中华民族的传统节日，节日期间大家都有吃粽子的习惯．某超市去年销售蛋黄粽、肉粽、豆沙粽的数量比为3：5：2．根据市场调查，超市决定今年在去年销售量的基础上进货，肉粽增加20%、豆沙粽减少10%、蛋黄粽不变．为促进销售，将全部粽子包装成三种礼盒，礼盒A有2个蛋黄粽、4个肉粽、2个豆沙粽，礼盒B有3个蛋黄粽、3个肉粽、2个豆沙粽，礼盒C有2个蛋黄粽、5个肉粽、1个豆沙粽，其中礼盒A和C的总数不超过200盒，礼盒B和C的总数超过210盒．每个蛋黄粽、肉粽、豆沙粽的售价分别为6元、5元、4元，且A、B、C三种礼盒的包装费分别为10元、12元、9元（礼盒售价为粽子价格加上包装费）．若这些礼盒全部售出，则销售额为_____元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学为了丰富学生的课余生活，准备从体育用品商店一次性购买若干个排球和篮球，若购买2个排球和1个篮球共需190元.购买3个排球和2个篮球共需330元.

    （1）购买一个排球、一个篮球各需多少元？

    （2）根据该校的实际情况，需从体育用品商店一次性购买排球和篮球共100个，要求购买排球和篮球的总费用不超过6500元，这所中学最多可以购买多少个篮球？

    查看答案和解析>>

    同步练习册答案