
【题目】某中学为了丰富学生的课余生活,准备从体育用品商店一次性购买若干个排球和篮球,若购买2个排球和1个篮球共需190元.购买3个排球和2个篮球共需330元.
(1)购买一个排球、一个篮球各需多少元?
(2)根据该校的实际情况,需从体育用品商店一次性购买排球和篮球共100个,要求购买排球和篮球的总费用不超过6500元,这所中学最多可以购买多少个篮球?
【答案】(1)购买一个排球需50元、一个篮球需90元;(2)这所中学最多可以购买37个篮球.
【解析】
(1)设每个排球x元,每个篮球y元,根据“购买2个排球和1个篮球共需190元,购买3个排球和2个篮球共需330元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买篮球a个,则购买排球(100-a)个,根据总价=单价×数量结合购买排球和篮球的总费用不超过6500元,即可得出关于a的一元一次不等式,解之取其中的最大值整数值即可得出结论.
解:(1)设每个排球x元,每个篮球y元,
依题意,得:![]()
解得:![]()
答:每个排球50元,每个篮球90元.
(2)设购买篮球a个,则购买排球(100-a)个,
依题意,得:90a+50(100-a)≤6500,
解得:a≤37.5.
∵a为整数,
∴a最大取37.
答:最多可以买37个篮球.


科目:初中数学 来源: 题型:
【题目】1955年,印度数学家卡普耶卡(![]() )研究了对四位自然数的一种变换:任给出四位数
)研究了对四位自然数的一种变换:任给出四位数![]() ,用
,用![]() 的四个数字由大到小重新排列成一个四位数
的四个数字由大到小重新排列成一个四位数![]() ,再减去它的反序数
,再减去它的反序数![]() (即将
(即将![]() 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数![]() ,然后继续对
,然后继续对![]() 重复上述变换,得数
重复上述变换,得数![]() ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论![]() 是多大的四位数,只要四个数字不全相同,最多进行
是多大的四位数,只要四个数字不全相同,最多进行![]() 次上述变换,就会出现变换前后相同的四位数
次上述变换,就会出现变换前后相同的四位数![]() ,这个数称为
,这个数称为![]() 变换的核.则四位数9631的
变换的核.则四位数9631的![]() 变换的核为______.
变换的核为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD,如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为16![]() 米,加固后大坝的横截面为梯形ABED,CE的长为8米.
米,加固后大坝的横截面为梯形ABED,CE的长为8米.
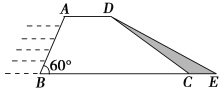
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE的坡度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将![]() 经过一次平移后得到
经过一次平移后得到![]() ,图中标出了点
,图中标出了点![]() 的对应点
的对应点![]() .(小正方形边长为1,
.(小正方形边长为1,![]() 的顶点均为小正方形的顶点)
的顶点均为小正方形的顶点)
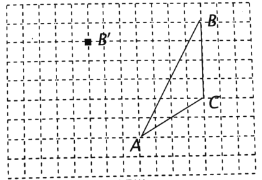
(1)补全![]() ;
;
(2)画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 中
中![]() 边上的高线
边上的高线![]() ;
;
(4)![]() 的面积为_____.
的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班同学为了解2017年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量 | 频数(户数) | 百分比 |
| 6 |
|
|
| |
| 16 |
|
| 10 |
|
| 4 | |
| 2 |
|

(1)请将下列频数分布表和频数分布直方图补充完整;
(2)求该小区月均用水量不超过![]() 的家庭占被调查家庭总数的百分比;
的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过![]() 的家庭数.
的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于给定的两点
中,对于给定的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,使得
,使得![]() 的面积等于1,即
的面积等于1,即![]() ,则称点
,则称点![]() 为线段
为线段![]() 的“单位面积点”.
的“单位面积点”.
解答下列问题:
如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() .
.
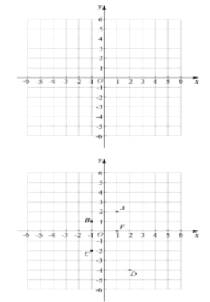
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,线段
中,线段![]() 的“单位面积点”是______.
的“单位面积点”是______.
(2)已知点![]() ,
,![]() ,点
,点![]() ,
,![]() 是线段
是线段![]() 的两个“单位面积点”,点
的两个“单位面积点”,点![]() 在
在![]() 的延长线上,若
的延长线上,若![]() ,直接写出点
,直接写出点![]() 纵坐标的取值范围.
纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?
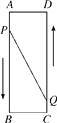
查看答案和解析>>
科目:初中数学 来源: 题型:
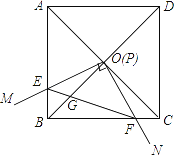
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是________.
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF= ![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com