
ЁОЬтФПЁПЖЫЮчНкЪЧжаЛЊУёзхЕФДЋЭГНкШеЃЌНкШеЦкМфДѓМвЖМгаГдєезгЕФЯАЙпЃЎФГГЌЪаШЅФъЯњЪлЕАЛЦєеЁЂШтєеЁЂЖЙЩГєеЕФЪ§СПБШЮЊ3ЃК5ЃК2ЃЎИљОнЪаГЁЕїВщЃЌГЌЪаОіЖЈНёФъдкШЅФъЯњЪлСПЕФЛљДЁЩЯНјЛѕЃЌШтєедіМг20%ЁЂЖЙЩГєеМѕЩй10%ЁЂЕАЛЦєеВЛБфЃЎЮЊДйНјЯњЪлЃЌНЋШЋВПєезгАќзАГЩШ§жжРёКаЃЌРёКаAга2ИіЕАЛЦєеЁЂ4ИіШтєеЁЂ2ИіЖЙЩГєеЃЌРёКаBга3ИіЕАЛЦєеЁЂ3ИіШтєеЁЂ2ИіЖЙЩГєеЃЌРёКаCга2ИіЕАЛЦєеЁЂ5ИіШтєеЁЂ1ИіЖЙЩГєеЃЌЦфжаРёКаAКЭCЕФзмЪ§ВЛГЌЙ§200КаЃЌРёКаBКЭCЕФзмЪ§ГЌЙ§210КаЃЎУПИіЕАЛЦєеЁЂШтєеЁЂЖЙЩГєеЕФЪлМлЗжБ№ЮЊ6дЊЁЂ5дЊЁЂ4дЊЃЌЧвAЁЂBЁЂCШ§жжРёКаЕФАќзАЗбЗжБ№ЮЊ10дЊЁЂ12дЊЁЂ9дЊЃЈРёКаЪлМлЮЊєезгМлИёМгЩЯАќзАЗбЃЉЃЎШєетаЉРёКаШЋВПЪлГіЃЌдђЯњЪлЖюЮЊ_____дЊЃЎ
ЁОД№АИЁП12312
ЁОНтЮіЁП
ЩшГЌЪаШЅФъЯњЪлЕАЛЦєеЕФЪ§СПЯњЪлЗжБ№ЮЊ3xИіЃЌЩшЯњЪлСЫAЁЂBЁЂCШ§жжРёКаЕФЪ§СПЗжБ№ЮЊaКаЃЌbКаЃЌcКаЃЌИљОнЬтвтСаГіЗНГЬзщЃЌгУxБэЪОaЁЂbЁЂcЃЌдйИљОнЁАРёКаAКЭCЕФзмЪ§ВЛГЌЙ§200КаЃЌРёКаBКЭCЕФзмЪ§ГЌЙ§210КаЃЌСаГіxЕФВЛЕШЪНзщЃЌЧѓЕУxЕФШЁжЕЗЖЮЇЃЌдйИљОнРёКаЪ§гыєезгЪ§СПЮЊећЪ§ЃЌЧѓЕУxЕФжЕЃЌНјЖјБуПЩЧѓЕУНсЙћЃЎ
НтЃКЩшГЌЪаШЅФъЯњЪлЕАЛЦєеЁЂШтєеЁЂЖЙЩГєеЕФЪ§СПЯњЪлЗжБ№ЮЊ3xИіЃЌ5xИіЃЌ2xИіЃЌдђНёФъИУГЌЪаЯњЪлЕАЛЦєеЁЂШтєеЁЂЖЙЩГєеЕФЪ§СПЯњЪлЗжБ№ЮЊ3xИіЃЌЃЈ1+20%ЃЉЁС5xЃН6xИіЃЌЃЈ1Љ10%ЃЉЁС2xЃН1.8xИіЃЌЩшЯњЪлСЫAЁЂBЁЂCШ§жжРёКаЕФЪ§СПЗжБ№ЮЊaКаЃЌbКаЃЌcКаЃЌИљОнЬтвтЕУЃЌ
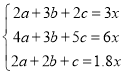 ЃЌ
ЃЌ
НтЕУЃЌ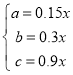 ЃЌ
ЃЌ
ЁпРёКаAКЭCЕФзмЪ§ВЛГЌЙ§200КаЃЌРёКаBКЭCЕФзмЪ§ГЌЙ§210КаЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпaЃН0.15xЁЂbЃН0.3xЁЂcЃН0.9xЁЂ1.8xЖМЮЊећЪ§ЃЌ
ЁрxБиЮЊ20ЕФБЖЪ§ЃЌ
ЁрxЃН180ЃЌ
ЁрaЃН27ЃЌbЃН54ЃЌcЃН162ЃЌ
ЁретаЉРёКаШЋВПЪлГіЕФЯњЪлЖюЮЊЃКЃЈ2ЁС6+4ЁС5+2ЁС4+10ЃЉa+ЃЈ3ЁС6+3ЁС5+2ЁС4+12ЃЉb+ЃЈ2ЁС6+5ЁС5+1ЁС4ЃЉcЃН50a+53b+50cЃН50ЁС27+53ЁС54+50ЁС162ЃН12312ЃЌ
ЙЪД№АИЮЊЃК12312ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌPЪЧЖдНЧЯпACЩЯЕФвЛЕуЃЌЕуEдкBCЕФбгГЄЯпЩЯЃЌЧвPE=PBЃЎ
ЃЈ1ЃЉЕБPC=CEЪБЃЌЧѓЁЯCDPЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЪдгУЕШЪНБэЪОЯпЖЮPBЁЂBCЁЂCEжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП1955ФъЃЌгЁЖШЪ§бЇМвПЈЦевЎПЈЃЈ![]() ЃЉбаОПСЫЖдЫФЮЛздШЛЪ§ЕФвЛжжБфЛЛЃКШЮИјГіЫФЮЛЪ§
ЃЉбаОПСЫЖдЫФЮЛздШЛЪ§ЕФвЛжжБфЛЛЃКШЮИјГіЫФЮЛЪ§![]() ЃЌгУ
ЃЌгУ![]() ЕФЫФИіЪ§зжгЩДѓЕНаЁжиаТХХСаГЩвЛИіЫФЮЛЪ§
ЕФЫФИіЪ§зжгЩДѓЕНаЁжиаТХХСаГЩвЛИіЫФЮЛЪ§![]() ЃЌдйМѕШЅЫќЕФЗДађЪ§
ЃЌдйМѕШЅЫќЕФЗДађЪ§![]() ЃЈМДНЋ
ЃЈМДНЋ![]() ЕФЫФИіЪ§зжгЩаЁЕНДѓХХСаЃЌЙцЖЈЗДађКѓШєзѓБпЪ§зжга0ЃЌдђНЋ0ШЅЕєдЫЫуЃЌБШШч0001ЃЌМЦЫуЪБАД1МЦЫуЃЉЃЌЕУГіЪ§
ЕФЫФИіЪ§зжгЩаЁЕНДѓХХСаЃЌЙцЖЈЗДађКѓШєзѓБпЪ§зжга0ЃЌдђНЋ0ШЅЕєдЫЫуЃЌБШШч0001ЃЌМЦЫуЪБАД1МЦЫуЃЉЃЌЕУГіЪ§![]() ЃЌШЛКѓМЬајЖд
ЃЌШЛКѓМЬајЖд![]() жиИДЩЯЪіБфЛЛЃЌЕУЪ§
жиИДЩЯЪіБфЛЛЃЌЕУЪ§![]() ЃЌЁЃЌШчДЫНјааЯТШЅЃЌПЈЦевЎПЈЗЂЯжЃЌЮоТл
ЃЌЁЃЌШчДЫНјааЯТШЅЃЌПЈЦевЎПЈЗЂЯжЃЌЮоТл![]() ЪЧЖрДѓЕФЫФЮЛЪ§ЃЌжЛвЊЫФИіЪ§зжВЛШЋЯрЭЌЃЌзюЖрНјаа
ЪЧЖрДѓЕФЫФЮЛЪ§ЃЌжЛвЊЫФИіЪ§зжВЛШЋЯрЭЌЃЌзюЖрНјаа![]() ДЮЩЯЪіБфЛЛЃЌОЭЛсГіЯжБфЛЛЧАКѓЯрЭЌЕФЫФЮЛЪ§
ДЮЩЯЪіБфЛЛЃЌОЭЛсГіЯжБфЛЛЧАКѓЯрЭЌЕФЫФЮЛЪ§![]() ЃЌетИіЪ§ГЦЮЊ
ЃЌетИіЪ§ГЦЮЊ![]() БфЛЛЕФКЫ.дђЫФЮЛЪ§9631ЕФ
БфЛЛЕФКЫ.дђЫФЮЛЪ§9631ЕФ![]() БфЛЛЕФКЫЮЊ______.
БфЛЛЕФКЫЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
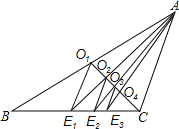
ЁОЬтФПЁПШчЭМЃЌвбжЊCO1ЪЧЁїABCЕФжаЯпЃЌЙ§ЕуO1зїO1E1ЁЮACНЛBCгкЕуE1ЃЌСЌНгAE1НЛCO1гкЕуO2ЃЛЙ§ЕуO2зїO2E2ЁЮACНЛBCгкЕуE2ЃЌСЌНгAE2НЛCO1гкЕуO3ЃЛЙ§ЕуO3зїO3E3ЁЮACНЛBCгкЕуE3ЃЌЁЃЌШчДЫМЬајЃЌПЩвдвРДЮЕУЕНЕуO4ЃЌO5ЃЌЁЃЌOnКЭЕуE4ЃЌE5ЃЌЁЃЌEnЃЎдђOnEn=ЁЁЁЁACЃЎЃЈгУКЌnЕФДњЪ§ЪНБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
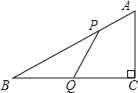
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10ЃЌBC=8ЃЌPЁЂQЗжБ№ЪЧABЁЂBCБпЩЯЕФЕуЃЌЧвAP=BQ=a ЃЈЦфжа0ЃМaЃМ8ЃЉЃЎ
ЃЈ1ЃЉШєPQЁЭBCЃЌЧѓaЕФжЕЃЛ
ЃЈ2ЃЉШєPQ=BQЃЌАбЯпЖЮCQШЦзХЕуQа§зЊ180ЁуЃЌЪдХаБ№ЕуCЕФЖдгІЕуCЁЏЪЧЗёТфдкЯпЖЮQBЩЯЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019Фъ4дТЃЌЮїДѓИНжаГѕ2019МЖжаеаЬхг§ПМЪдвбОЫГРћНсЪјЃЌдкЫљгаЪІЩњЙВЭЌХЌСІЯТЃЌШЁЕУСЫРњЪЗадЕФКУГЩМЈЃЎГѕЖўаЁУїЮЊСЫНтГѕШ§ИчИчНуНуУЧжаеаЬхг§ПМЪдГЩМЈЕФЧщПіЃЌВЩШЁГщбљЕїВщЕФЗНЗЈЃЌДгФъМЖИїАрЫцЛњЕїВщСЫШєИЩУћЭЌбЇЕФЬхПМГЩМЈЃЌВЂНЋЕїВщНсЙћНјааСЫећРэЃЌЗжГЩСЫ5ИіаЁзщЃЌИљОнЬхПМГЩМЈжЦЖЈГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМ
Ьхг§ГЩМЈЦЕЪ§ЗжВМБэ
зщБ№ | ГЩМЈЃЈxЗжЃЉ | ЦЕЪ§ | ЦЕТЪ |
A | 35ЃМxЁм38 | 1 | |
B | 38ЃМxЁм41 | 0.05 | |
C | 41ЃМxЁм44 | ||
D | 44ЃМxЁм47 | 6 | |
E | 47ЃМxЁм50 |
ЃЈ1ЃЉдкетДЮПМВьжаЃЌЙВЕїВщСЫЁЁ ЁЁУћбЇЩњЃЛВЂЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉБЛЕїВщЕФбЇЩњжаЃЌга30ШЫЪЧТњЗж50ЗжЃЌШєЮїДѓИНжаГѕ2019МЖШЋФъМЖга1100ЖрУћбЇЩњЃЌЧыЙРМЦИУФъМЖЬхПМГЩМЈТњЗжЕФзмШЫЪ§дМгаЖрЩйУћЃП
ЃЈ3ЃЉГѕШ§ИчИчНуНуУЧЬхВтШЁЕУЕФЛдЛЭГЩМЈШУГѕЖўЕФбЇЕмбЇУУУЧаХаФДѓдіЃЌЮЊСЫЕїЖЏГѕЖўбЇзгЬјЩўЛ§МЋадЃЌГѕЖўФъМЖНЋОйаа1ЗжжгЬјЩўБШШќЃЌУПАрЭЦМівЛШЫВЮШќЃЌаЁУїЫљдкЕФАрМЖРюНмКЭГТСССНШЫОљЯыБЈУћВЮШќЃЌЮЊСЫЙЋЦНбЁАЮЃЌАржїШЮШУаЁУїЭГМЦСЫСНШЫНќ10ДЮЕФЬјЩўГЩМЈЃЈЕЅЮЛЃКИі/ЗжЃЉЃЌШчЯТЃК
РюНмГЩМЈЃЈИі/ЗжЃЉ | 170 | 175 | 180 | 190 | 195 | |||||
ДЮЪ§ | l | 1 | 3 | 2 | 3 | |||||
ГТССГЩМЈЃЈИі/ЗжЃЉ | 165 | 180 | 190 | 195 | 200 | |||||
ДЮЪ§ | 2 | 2 | 3 | 2 | 1 | |||||
дђРюНм10ДЮГЩМЈЕФжаЮЛЪ§ЪЧЁЁ ЁЁЃЛГТСС10ДЮГЩМЈЕФжкЪ§ЪЧЁЁ ЁЁЃЌЧыФуЭЈЙ§МЦЫуСНЮЛЭЌбЇЕФЦНОљГЩМЈКЭЗНВюАяАржїШЮбЁвЛУћЭЌбЇВЮШќЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЁїABCжа,ЕуEдкACЩЯ,ЁЯAEB=ЁЯABC.
(1)ЭМ1жа,зїЁЯBACЕФНЧЦНЗжЯпAD,ЗжБ№НЛCBЁЂBEгкDЁЂFСНЕу,ЧѓжЄ:ЁЯEFD=ЁЯADCЃЛ
(2)ЭМ2жа,зїЁїABCЕФЭтНЧЁЯBAGЕФНЧЦНЗжЯпAD,ЗжБ№НЛCBЁЂBEЕФбгГЄЯпгкDЁЂFСНЕу,ЪдЬНОП(1)жаНсТлЪЧЗёШдГЩСЂ?ЮЊЪВУД?

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫЎРћВПУХЮЊМгЧПЗРбДЙЄзїЃЌОіЖЈЖдФГЫЎПтДѓАгНјааМгЙЬЃЌДѓАгЕФКсНиУцЪЧЬнаЮABCDЃЌШчЭМЫљЪОЃЌвбжЊгЫЎЦТУцABЕФГЄЮЊ16УзЃЌЁЯBЃН60ЁуЃЌБГЫЎЦТУцCDЕФГЄЮЊ16![]() УзЃЌМгЙЬКѓДѓАгЕФКсНиУцЮЊЬнаЮABEDЃЌCEЕФГЄЮЊ8УзЃЎ
УзЃЌМгЙЬКѓДѓАгЕФКсНиУцЮЊЬнаЮABEDЃЌCEЕФГЄЮЊ8УзЃЎ
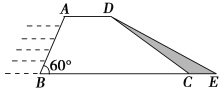
(1)вбжЊашМгЙЬЕФДѓАгГЄЮЊ150УзЃЌЧѓашвЊЬюЭСЪЏЗНЖрЩйСЂЗНУзЃП
(2)ЧѓМгЙЬКѓЕФДѓАгБГЫЎЦТУцDEЕФЦТЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
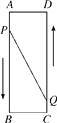
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЌBЃЌCЃЌDЮЊОиаЮЕФЫФИіЖЅЕуЃЌABЃН16 cmЃЌADЃН6 cmЃЌЖЏЕуPЃЌQЗжБ№ДгЕуAЃЌCЭЌЪБГіЗЂЃЌЕуPвд3 cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌвЛжБЕНЕуBЮЊжЙЃЌЕуQвд2 cm/sЕФЫйЖШЯђЕуDвЦЖЏЃЌЕБЕуPЭЃжЙдЫЖЏЪБЃЌЕуQвВЭЃжЙдЫЖЏЃЎЮЪЃК
(1)PЃЌQСНЕуДгПЊЪМГіЗЂЖрГЄЪБМфЪБЃЌЫФБпаЮPBCQЕФУцЛ§ЪЧ33 cm2?
(2)PЃЌQСНЕуДгПЊЪМГіЗЂЖрГЄЪБМфЪБЃЌЕуPгыЕуQжЎМфЕФОрРыЪЧ10 cm?
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com