
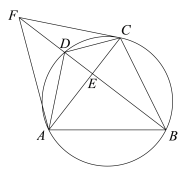
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
【答案】(1)见解析;(2) tan∠BAD=![]() .
.
【解析】
(1)根据等腰三角形的性质得出∠ABC=∠ACB,根据圆心角、弧、弦的关系得到![]() =
=![]() ,即可得到∠ABC=∠ADB,根据三角形内角和定理得到∠ABC=
,即可得到∠ABC=∠ADB,根据三角形内角和定理得到∠ABC=![]() (180°∠BAC)=90°
(180°∠BAC)=90°![]() ∠BAC,∠ADB=90°∠CAD,从而得到
∠BAC,∠ADB=90°∠CAD,从而得到![]() ∠BAC=∠CAD,即可证得结论;
∠BAC=∠CAD,即可证得结论;
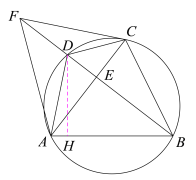
(2)易证得BC=CF=4![]() ,即可证得AC垂直平分BF,证得AB=AF=10,根据勾股定理求得AE、CE、BE,根据相交弦定理求得DE,即可求得BD,然后根据三角形面积公式求得DH,进而求得AH,解直角三角形求得tan∠BAD的值.
,即可证得AC垂直平分BF,证得AB=AF=10,根据勾股定理求得AE、CE、BE,根据相交弦定理求得DE,即可求得BD,然后根据三角形面积公式求得DH,进而求得AH,解直角三角形求得tan∠BAD的值.
解:(1)∵AB=AC,
∴![]() =
=![]() ,∠ABC=∠ACB,
,∠ABC=∠ACB,
∴∠ABC=∠ADB,∠ABC=![]() (180°∠BAC)=90°
(180°∠BAC)=90°![]() ∠BAC,
∠BAC,
∵BD⊥AC,
∴∠ADB=90°∠DAC,
∴![]() ∠BAC=∠DAC,
∠BAC=∠DAC,
∴∠BAC=2∠DAC;
(2)∵DF=DC,
∴∠BFC=![]() ∠BDC=
∠BDC=![]() ∠BAC=∠FBC,
∠BAC=∠FBC,
∴CB=CF,
又BD⊥AC,
∴AC是线段BF的中垂线,AB= AF=10, AC=10.
又BC=4![]() ,
,
设AE=x, CE=10-x,
AB2-AE2=BC2-CE2, 100-x2=80-(10-x)2, x=6
∴AE=6,BE=8,CE=4,
∴DE=![]() =
=![]() =3,
=3,
∴BD=BE+DE=3+8=11,
作DH⊥AB,垂足为H,
∵![]() ABDH=
ABDH=![]() BDAE,
BDAE,
∴DH=![]() ,
,
∴BH=![]() ,
,
∴AH=ABBH=10![]() ,
,
∴tan∠BAD=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】2020年伊始,全国发生了传播速度快、感染范围广、防控难度大的新冠肺炎疫情.根据教育部提出的2020年春节延期开学,“停课不停学”的相关要求,很多学校开展了线上授课相关工作.为了更好地提高学生线上授课的效果,某中学进行了线上授课问卷调查.其中一项调查是:你认为影响师生互动的最主要因素是A.教师的授课理念;B.网络配麦等硬件问题;C.科目特点;D.学生的配合情况,针对这个题目,问卷时要求每位同学必须且只能选择其中一项.现随机抽取了若干名学生的调查问卷,将所得数据进行整理,制成如下条形统计图和扇形统计图.
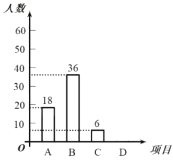
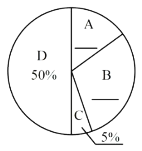
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生中认为影响师生互动最主要因素的众数为____________;
(3)已知该校有2400名学生,请你估计该校学生中认为影响师生互动的最主要因素是“C.科目特点”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
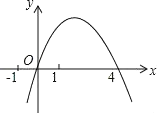
A.t>﹣5B.﹣5<t<3C.3<t≤4D.﹣5<t≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
给出以下结论:(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;(2)当﹣![]() <x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
<x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 在射线
在射线![]() 上.
上.
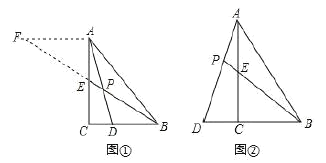
猜想:如图①,点![]() 在
在![]() 边上,
边上,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,则
,则![]() 的值为 .
的值为 .
探究:如图②,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
, ![]() ,求
,求![]() 的值.
的值.
应用:在探究的条件下,若![]() ,
,![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
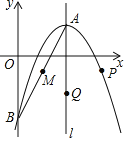
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中.抛物线y=﹣x2+4x+3与y轴交于点A,抛物线的对称轴与x轴交于点B,连接AB,将△OAB绕着点B顺时针旋转得到△O'A'B.
(1)用配方法求抛物线的对称轴并直接写出A,B两点的坐标;
(2)如图1,当点A'第一次落在抛物线上时,∠O'BO=n∠OAB,请直接写出n的值;
(3)如图2,当△OAB绕着点B顺时针旋转60°,直线A'O'交x轴于点M,求△A'MB的面积;
(4)在旋转过程中,连接OO',当∠O'OB=∠OAB时.直线A'O'的函数表达式是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com