
【题目】在平面直角坐标系中.抛物线y=﹣x2+4x+3与y轴交于点A,抛物线的对称轴与x轴交于点B,连接AB,将△OAB绕着点B顺时针旋转得到△O'A'B.
(1)用配方法求抛物线的对称轴并直接写出A,B两点的坐标;
(2)如图1,当点A'第一次落在抛物线上时,∠O'BO=n∠OAB,请直接写出n的值;
(3)如图2,当△OAB绕着点B顺时针旋转60°,直线A'O'交x轴于点M,求△A'MB的面积;
(4)在旋转过程中,连接OO',当∠O'OB=∠OAB时.直线A'O'的函数表达式是 .

【答案】(1)对称轴为x=2,A(0,3),B(2,0);(2)n=2;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)配方写成顶点式即可得到对称轴,从而求出B的坐标;
(2)利用抛物线的对称性易知△BFA′≌△BOA,从而推导出∠O'BO与∠OAB的关系;
(3)延长A'O'与x轴交于M,构造特殊的直角三角形,先求出MO′,再求△A′MB的面积;
(4)连接OO'与AB交于C,作O'E⊥x轴于E,可得△AOB∽△OEO′~△OCB,再利用对应边成比例可求出OC,O′E,OE,再求出A′O′的解析式.
(1)y=﹣x2+4x+3=﹣(x﹣2)2+7
所以对称轴为x=2,所以B(2,0)
当x=0时,y=3,
所以A(0,3);
(2)作A'F⊥x轴于F,由于二次函数的对称性,
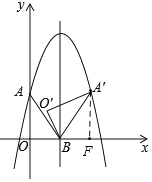
得OB=FB,AO=A'F
∵∠AOB=∠A'FB=90°,
∴△BFA'≌△BOA,设∠OAB=α,
则∠O′BO=180°(∠FBA′+∠O′BA′)=180°(90°-α+90°-α)=2α,
所以n=2;
(3)延长A'O'与x轴交于M,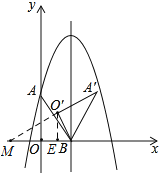
∵∠MBO′=60°,O′B=OB=2,
∴MO′=2![]()
∴S△A′MB=![]() (MO′+O′A′)O′B=2
(MO′+O′A′)O′B=2![]() +3;
+3;
(4)连接OO'与AB交于C,作O'E⊥x轴于E,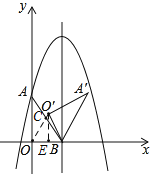
所以△AOB∽△OEO′~△OCB,
所以![]() ,
,
∴OC=![]() ,
,
同理可得:O′E=![]() ,OE=
,OE=![]() ,
,
所以O′(![]() ),B(2,0),
),B(2,0),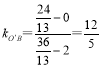 ,
,
所以kO′A′=![]() ,
,
所以A′O′:y=![]() x+3.
x+3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
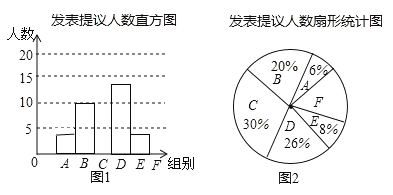
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得样本容量为 ,并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中![]() ).
).
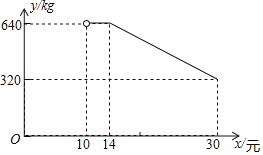
(1)直接写出y与x之间的函数关系式及自变量的取值范围.
(2)若农贸公司每天销售该特产的利润要达到3100元,则销售单价x应定为多少元?
(3)设每天销售该特产的利润为W元,若![]() ,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下定义:对于⊙O的弦MN和⊙O外一点P(M,O,N三点不共线,且点P,O在直线MN的异侧),当∠MPN+∠MON=180°时,则称点P是线段MN关于点O的关联点.图1是点P为线段MN关于点O的关联点的示意图.
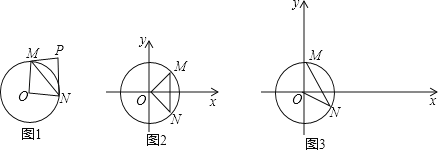
在平面直角坐标系xOy中,⊙O的半径为1.
(1)如图2,已知M(![]() ,
,![]() ),N(
),N(![]() ,﹣
,﹣![]() ),在A(1,0),B(1,1),C(
),在A(1,0),B(1,1),C(![]() ,0)三点中,是线段MN关于点O的关联点的是 ;
,0)三点中,是线段MN关于点O的关联点的是 ;
(2)如图3,M(0,1),N(![]() ,﹣
,﹣![]() ),点D是线段MN关于点O的关联点.
),点D是线段MN关于点O的关联点.
①∠MDN的大小为 ;
②在第一象限内有一点E(![]() m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
③点F在直线y=﹣![]() x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
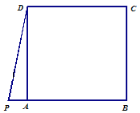
【题目】如图,正方形 ABCD 中,P 是 BA 延长线上一点,且PDA (0 45).点 A,点 E 关于 DP 对称,连接 ED,EP ,并延长 EP 交射线CB 于点 F ,连接 DF .
(1)请按照题目要求补全图形.
(2)求证:∠EDF=∠CDF
(3)求∠EDF(含有 的式子表示);
(4)过 P 做PH⊥DP交 DF 于点 H ,连接 BH , 猜想 AP 与 BH 的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC.
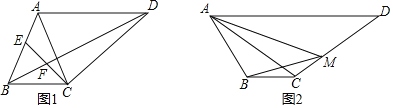
(1)如图1,AB=AC,点E为AB上一点,∠BEC=∠ACD.
①求证:ABBC=ADBE;
②连接BD交CE于F,试探究CF与CE的数量关系,并证明;
(2)如图2,若AB≠AC,点M在CD上,cos∠DAC=cos∠BMA=![]() ,AC=CD=3MC,ADBC=12,直接写出BC的长.
,AC=CD=3MC,ADBC=12,直接写出BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com