
【题目】如图,四边形ABCD中,AD∥BC.
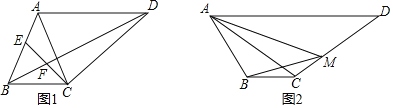
(1)如图1,AB=AC,点E为AB上一点,∠BEC=∠ACD.
①求证:ABBC=ADBE;
②连接BD交CE于F,试探究CF与CE的数量关系,并证明;
(2)如图2,若AB≠AC,点M在CD上,cos∠DAC=cos∠BMA=![]() ,AC=CD=3MC,ADBC=12,直接写出BC的长.
,AC=CD=3MC,ADBC=12,直接写出BC的长.
【答案】(1)①见解析,②CE=2CF,见解析;(2)![]()
【解析】
(1)①证明△BEC∽△ACD可得结论.
②结论:CE=2CF.利用相似三角形的性质证明CM=BE,再证明△MCF≌△BEF(ASA),推出CF=EF即可解决问题.
(2)如图2中,作CH⊥AD于H.证明△ABC∽△AMD,可得ACDM=BCAD=12,由AC=CD=3CM,推出6CM2=12,推出CM=![]() ,
,![]() ,解直角三角形求出AD即可解决问题.
,解直角三角形求出AD即可解决问题.
(1)①∵AD∥BC,
∴∠DAC=∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC=∠CAD,
∵∠BEC=∠ACD,
∴△BEC∽△ACD,
∴![]() ,
,
∴BCAC=ADBE,
∵AB=AC,
∴ABBC=ADBE.
②解:结论:CE=2CF.
理由:如图1中,作CM∥AB交BD于M,设BD交AC于N.
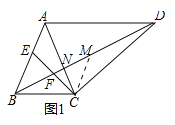
∵CM∥AB,
∴∠BAN=∠MCN,∠CMN=∠ABN,
∴△MCN∽△BAN,
∴![]() ,
,
∵AD∥BC,
∴∠NAD=∠NCB,∠AND=∠CNB,
∴△CNB∽△AND,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵AB=AC,
∴CM=BE,
∵CM∥BE,
∴∠CMF=∠BEF,∠BEF=∠MCF,
∴△MCF≌△BEF(ASA),
∴CF=EF,
∴CE=2CF.
(2)解:如图2中,作CH⊥AD于H.

∵AD∥BC,
∴∠CAD=∠ACB,
∵cos∠DAC=cos∠BMA,
∴∠DAC=∠AMB,
∴∠AMB=∠ACB,
∴A,B,C,M四点共圆,
∴∠BAC=∠BMC,
∵CA=CD,
∴∠CAD=∠D=∠AMB,
∵∠AMC=∠MAD+∠D=∠BMA+∠BMC,
∴∠BMC=∠MAD,
∴∠BAC=∠MAD
∵∠ACB=∠AMB=∠D,
∴△ABC∽△AMD,
∴![]() ,
,
∴ACDM=BCAD=12,
∵AC=CD=3CM,
∴6CM2=12,
∵CM>0,
∴CM=![]() ,
,
∴![]() ,
,
∵CH⊥AD,
∴AH=DH,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∵BCAD=12,
∴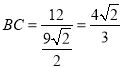 .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中.抛物线y=﹣x2+4x+3与y轴交于点A,抛物线的对称轴与x轴交于点B,连接AB,将△OAB绕着点B顺时针旋转得到△O'A'B.
(1)用配方法求抛物线的对称轴并直接写出A,B两点的坐标;
(2)如图1,当点A'第一次落在抛物线上时,∠O'BO=n∠OAB,请直接写出n的值;
(3)如图2,当△OAB绕着点B顺时针旋转60°,直线A'O'交x轴于点M,求△A'MB的面积;
(4)在旋转过程中,连接OO',当∠O'OB=∠OAB时.直线A'O'的函数表达式是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD 是菱形ABCD 的对角线,∠A=30°.
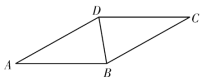
(1)请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,求∠DBF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
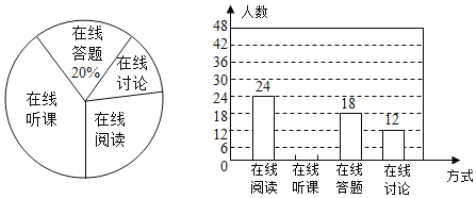
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生2700人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1,D1E1E2B2,A2B2C2D2,D2E3E4B3,A3B3C3D3…,按如图所示的方式放置,其中点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3,…,在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2018B2018C2018D2018边长是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张华为了测量重庆最高塔楼![]() 的高度,他从塔楼底部
的高度,他从塔楼底部![]() 出发,沿广场前进185米至点
出发,沿广场前进185米至点![]() ,继而沿坡度为
,继而沿坡度为![]() 的斜坡向下走65米到达码头
的斜坡向下走65米到达码头![]() ,然后在浮桥上继续前行110米至趸船
,然后在浮桥上继续前行110米至趸船![]() ,在
,在![]() 处小明操作一架无人勘测机,当无人勘测机飞行至点
处小明操作一架无人勘测机,当无人勘测机飞行至点![]() 的正上方点
的正上方点![]() 时,测得码头
时,测得码头![]() 的俯角为
的俯角为![]() ,楼顶
,楼顶![]() 的仰角为
的仰角为![]() ,点
,点![]() 在同一平面内,则塔楼
在同一平面内,则塔楼![]() 的高度约为( )(结果精确到1米,参考数据:
的高度约为( )(结果精确到1米,参考数据:![]() ,
,![]() ,
,![]()
![]() )
)
A.319米B.335米C.342米D.356米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com