
【题目】如图,△ABC中,⊙O是△ABC的内切圆,切点分别为D、E、F.
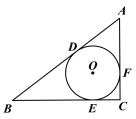
(1)已知∠C=90°.
①若BD=6,AD=4,则⊙O的半径r为 ,△ABC的面积为 ;
②若BD=m,AD=n,请用含m、n的代数式表示△ABC的面积;
(2)若![]() ,试判断△ABC的形状,并说明理由。
,试判断△ABC的形状,并说明理由。
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
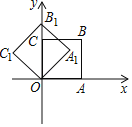
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
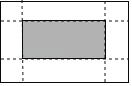
【题目】如图,有一张矩形纸片,长15cm,宽9cm,在它的四角各剪去一个同样的小正方形,然折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是48cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若![]() ,则
,则![]() 的值是 ___.
的值是 ___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点![]() 每个小方格的顶点叫格点
每个小方格的顶点叫格点![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
![]() 外接圆的圆心坐标是______;
外接圆的圆心坐标是______;
![]() 外接圆的半径是______;
外接圆的半径是______;
![]() 已知
已知![]() 与
与![]() 点D、E、F都是格点
点D、E、F都是格点![]() 成位似图形,则位似中心M的坐标是______;
成位似图形,则位似中心M的坐标是______;
![]() 请在网格图中的空白处画一个格点
请在网格图中的空白处画一个格点![]() ,使
,使![]() ∽
∽![]() ,且相似比为
,且相似比为![]() :1.
:1.

查看答案和解析>>
科目:初中数学 来源: 题型:
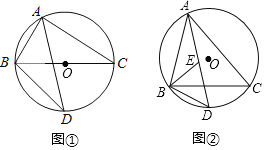
【题目】已知△ABC是⊙O的内接三角形,∠BAC的平分线交⊙O于点D.
(I)如图①,若BC是⊙O的直径,BC=4,求BD的长;
(Ⅱ)如图②,若∠ABC的平分线交AD于点E,求证:DE=DB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人:
(1)第一轮后患病的人数为 ;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
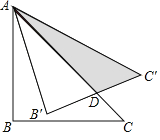
【题目】如图,等腰直角三角形ABC的直角边AB的长为![]() ,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于( )
,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com