
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点![]() 每个小方格的顶点叫格点
每个小方格的顶点叫格点![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
![]() 外接圆的圆心坐标是______;
外接圆的圆心坐标是______;
![]() 外接圆的半径是______;
外接圆的半径是______;
![]() 已知
已知![]() 与
与![]() 点D、E、F都是格点
点D、E、F都是格点![]() 成位似图形,则位似中心M的坐标是______;
成位似图形,则位似中心M的坐标是______;
![]() 请在网格图中的空白处画一个格点
请在网格图中的空白处画一个格点![]() ,使
,使![]() ∽
∽![]() ,且相似比为
,且相似比为![]() :1.
:1.

【答案】(1)(2,6);(2)![]() ; (3)(3,6) ;(4)见解析.
; (3)(3,6) ;(4)见解析.
【解析】
(1)根据作图,结合网格特点解答;
(2)根据线段垂直平分线的性质和三角形的外接圆的概念解答;
(3)根据位似变换和位似中心的概念解答;
(4)根据相似三角形的对应边的比相等,都等于相似比解答.
解:(1)如图1,
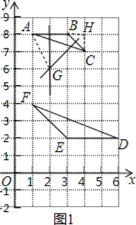
由作图可知△ABC外接圆的圆心坐标是(2,6),
故答案为:(2,6);
(2)作AB、BC的垂直平分线交于G,连接AG,
根据网格特点可知,点G的坐标为(2,6),
则AG=![]() =
=![]() ,
,
则△ABC外接圆的半径是![]() ,
,
故答案为:![]() ;
;
(3)如图2,连接BE、FC,
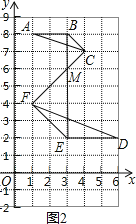
根据网格特点,BE与FC交于点M,
点M的坐标为(3,6),
根据位似中心的概念可知,位似中心M的坐标是(3,6),
故答案为:(3,6);
(4)由网格特点可知,AB=2,BC=![]() ,AC=
,AC=![]() ,
,
∵△A1B1C1∽△ABC,且相似比为![]() :1,
:1,
∴A1B1=2![]() ,B1C1=2,A1C1=2
,B1C1=2,A1C1=2![]() ,
,
所求的△A1B1C1如图3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
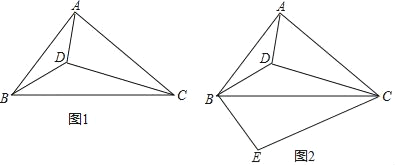
【题目】如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若ACBD=ADBC,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是_____km.

查看答案和解析>>
科目:初中数学 来源: 题型:
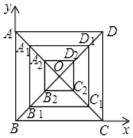
【题目】如图以正方形ABCD的B点为坐标原点.BC所在直线为x轴,BA所在直线为y轴,建立直角坐标系.设正方形ABCD的边长为6,顺次连接OA、OB、OC、OD的中点A1、B1、C1、D1,得到正方形A1B1C1D1,再顺次连接OA1、OB1、OC1、OD1的中点得到正方形A2B2C2D2.按以上方法依次得到正方形A1B1C1D1,……AnBnCnDn,(n为不小于1的自然数),设An点的坐标为(xn,yn),则xn+yn=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰![]() 和等腰
和等腰![]() ,其中
,其中![]() ,CD与BE、AE分别交于点P、
,CD与BE、AE分别交于点P、![]() 对于下列结论:
对于下列结论:
![]() ∽
∽![]() ;
;![]() ;
;![]() ;
;![]() .
.
其中正确的是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD 分别为两圆的弦,AC、BD 为两圆的公切线且相交于点 P.若 PC=2,DB=6,∠APB=90°.
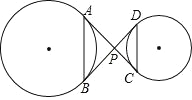
(1)求△PAB 的周长.
(2)求△PAB 与△PCD 的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:已知二次函数的图象与![]() 轴交于
轴交于![]() 和
和![]() 两点.交
两点.交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,![]() 是二次函数图象上的一对对称点,一次函数的图象过点
是二次函数图象上的一对对称点,一次函数的图象过点![]() ,
,![]()
(1)画出图象,并求二次函数的解析式.
(2)根据图象直接写出使一次函数值大于或等于二次函数值的![]() 的取值范围.
的取值范围.
(3)若直线与![]() 轴交点为
轴交点为![]() ,连接
,连接![]() ,
,![]() ,求三角形
,求三角形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com