
【题目】如图,O为正方形ABCD的对角线AC上一点,以O为圆心,OC的长为半径的![]() 与AB相切于点M.
与AB相切于点M.
![]() 求证:AD与
求证:AD与![]() 相切;
相切;
![]() 若
若![]() ,求图中阴影部分面积.
,求图中阴影部分面积.

【答案】(1)见解析;(2)2π-4.
【解析】
(1)过O作ON⊥AD于N,由垂直的定义得到∠ONA=90°,根据正方形的性质得到∠OAN=∠OAM=45°,根据切线的性质得到∠OMA=90°,根据全等三角形的性质得到ON=OM,于是得到结论;
(2)首先求出AE=AF,进而求出△CEF的面积,进而得出阴影部分的面积.
解: (1)证明:连接OM,过O作ON⊥AD于N,
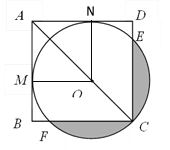
∴∠ONA=90°,
∵四边形ABCD是正方形,
∴∠OAN=∠OAM =45°,
∵AB与⊙O相切于M,
∴∠OMA=90°,
在△ONA与△OMA中,
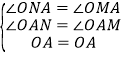 ,
,
∴△ONA≌△OMA,
∴ON=OM,
∴BC与⊙O相切;
(2)设⊙O的半径为r.
显然OM∥CB,
∴△AOM∽△ACB,
∴ ![]() ,即
,即![]() ,
,

解得r=2
故⊙O的半径为2;
连接EF,
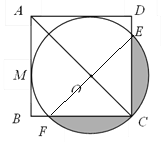
则EF是⊙O的直径,
∵AC是正方形ABCD的对角线,
∴∠DAC=45°,
∵CO=FO,
∴∠CFO=45°,
∴∠COF=90°,
则AE=AF,
∵EF=4,
∴CE=CF=2![]() ,
,
∴S△CEF=![]() ×2
×2![]() ×2
×2![]() =4,
=4,![]() =
=![]() =
=![]() ,
,
故阴影部分面积: ![]() -4.
-4.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
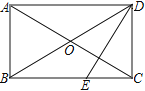
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点![]() 每个小方格的顶点叫格点
每个小方格的顶点叫格点![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
![]() 外接圆的圆心坐标是______;
外接圆的圆心坐标是______;
![]() 外接圆的半径是______;
外接圆的半径是______;
![]() 已知
已知![]() 与
与![]() 点D、E、F都是格点
点D、E、F都是格点![]() 成位似图形,则位似中心M的坐标是______;
成位似图形,则位似中心M的坐标是______;
![]() 请在网格图中的空白处画一个格点
请在网格图中的空白处画一个格点![]() ,使
,使![]() ∽
∽![]() ,且相似比为
,且相似比为![]() :1.
:1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列 材料,并解答总题:
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母x+1,可设![]()
则![]()
=![]()
∵对于任意![]() 上述等式成立
上述等式成立
∴![]() ,
,
解得![]() ,
,
∴![]()
这样,分式![]() 就拆分成一个整式
就拆分成一个整式![]() 与一个分式
与一个分式![]() 的和的形式.
的和的形式.
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式为___________;
拆分成一个整式与一个分式(分子为整数)的和的形式为___________;
(2)已知整数![]() 使分式
使分式![]() 的值为整数,则满足条件的整数
的值为整数,则满足条件的整数![]() =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=45°,CD⊥AB,垂足为点D,M为线段DB上一动点(不包括端点),点N在直线AC左上方且∠NCM=135°,CN=CM,如图①.
(1)求证:∠ACN=∠AMC;
(2)记△ANC得面积为5,记△ABC得面积为5.求证:![]() ;
;
(3)延长线段AB到点P,使BP=BM,如图②.探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M,AN=CP始终成立?(写出探究过程)
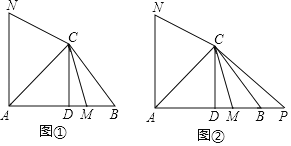
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题
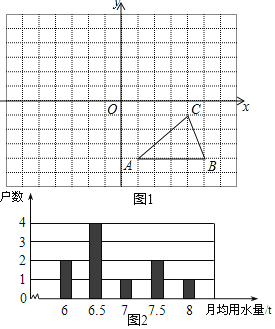
(1)如图1,方格纸中的每个小方格都是边长为1个单位长的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①作出△ABC关于x轴对称的△A1B1C1;
②如果P点的纵坐标为3,且P点到直线AA的距离为5,请直接写出点P的坐标.
(2)我国是世界上严重缺水的国家之一为了倡导“节约用水,从我做起”,小丽同学在她家所在小区的200住户中,随机调查了10个家庭在2019年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图2
①求这10个样本数据的平均数;
②以上面的样本平均数为依据,自来水公司按2019年该小区户月均用水量下达了2020年的用水计划(超计划要执行阶梯式标准收费)请计算该小区2020年的计划用水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com