
【题目】在半径为1的⊙O中,弦AB=![]() ,AC=
,AC=![]() ,那么∠BAC=___________.
,那么∠BAC=___________.
【答案】15°或75°
【解析】
先根据题意画出图形,分别作AC、AB的垂线,连接OA,再根据锐角三角函数的定义求出∠AOD及∠AOE的度数,根据直角三角形的性质即可得出结论.
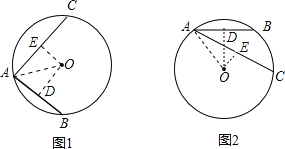
①如图1,两弦在圆心的异侧时,过O作OD⊥AB于点D,OE⊥AC于点E,连接OA,
∵![]()
∴![]()
根据直角三角形中三角函数的值可知:sin∠AOD=![]()
∴∠AOD=45°,
∵sin∠AOE![]()
∴∠AOE=60°,
∴∠OAD=90°∠AOD=45°,∠OAC=90°∠AOE=30°
∴∠BAC=∠OAD+∠OAC=45°+30°=75°;
②如图2,当两弦在圆心的同侧时同①可知∠AOD=45°,∠AOE=60°,
∴∠AOE=60°,
∴∠OAC=90°∠AOE=90°60°=30°,∠OAB=90°∠AOD=90°45°=45°,
∴∠BAC=∠OAB∠OAC=45°30°=15°,
即∠BAC=15°或75°
故答案为:15°或75°


科目:初中数学 来源: 题型:
【题目】给出下列命题:①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;④△ABC中,若a:b:c=1:2:![]() ,则这个三角形是直角三角形,其中,正确命题为_____(选填序号).
,则这个三角形是直角三角形,其中,正确命题为_____(选填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
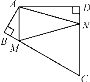
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
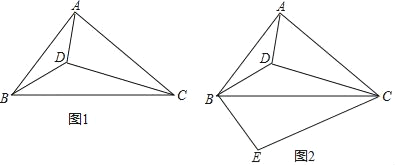
【题目】如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若ACBD=ADBC,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
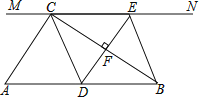
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由.
(2)在(1)的条件下,当∠A=__________°时,四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弧CD⊥AB,垂足为H,P为弧AD上一点,连接PA、PB,PB交CD于E.
(1)如图(1)连接PC、CB,求证:∠BCP=∠PED;
(2)如图(2)过点P作⊙O的切线交CD的延长线于点E,过点A向PF引垂线,垂足为G,求证:∠APG=![]() ∠F;
∠F;
(3)如图(3)在图(2)的条件下,连接PH,若PH=PF,3PF=5PG,BE=2![]() ,求⊙O的直径AB.
,求⊙O的直径AB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com