【题目】如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC，CD上分别找一点M，N，使△AMN周长最小时，则∠AMN＋∠ANM的度数是________
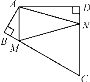
【答案】120°
【解析】根据要使△AMN的周长最小，即利用点的对称，使三角形的三边在同一直线上，作出A关于BC和CD的对称点A′，A″，结合图形及已知条件，即可求出结果.
如图所示，当三角形三边在同一条直线上周长最短，作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN周长的最小值.作DA延长线AH，
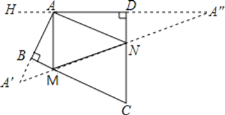
∵∠DAB=120°，
∴∠HAA′=60°，
∴∠AA′M+∠A″=∠HAA′=60°.
∵∠MA′A=∠MAA′，∠NAD=∠A″，且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°.
故答案为：120°.
科目：初中数学 来源： 题型：
【题目】给出下列命题：①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；②三角形的三边a、b、c满足a2+c2=b2，则∠C=90°；③命题“菱形的四条边都相等”的逆命题是四条边相等的四边形是菱形．④△ABC中，若 a：b：c=1：2：
，则这个三角形是直角三角形．其中，正确命题的个数为（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
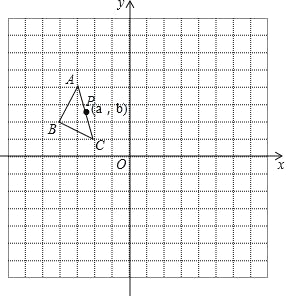
【题目】如图，在平面直角坐标系中有△ABC，其中A（﹣3，4），B（﹣4，2），C（﹣2，1）．把△ABC绕原点顺时针旋转90°，得到△A1B1C1．再把△A1B1C1向左平移2个单位，向下平移5个单位得到△A2B2C2．
（1）画出△A1B1C1和△A2B2C2．
（2）直接写出点B1、B2坐标．
（3）P（a，b）是△ABC的AC边上任意一点，△ABC经旋转平移后P对应的点分别为P1、P2，请直接写出点P1、P2的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
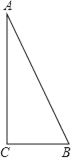
【题目】如图，在Rt△ABC中，∠C＝90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
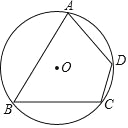
【题目】如图，已知四边形 ABCD 内接于⊙O，且已知∠ADC=120°；请仅用无刻度直尺作出一个30°的圆周角．要求：
(1)保留作图痕迹，写出作法，写明答案；
(2)证明你的作法的正确性．
查看答案和解析>>
科目：初中数学 来源： 题型：
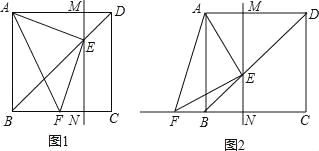
【题目】如图，点 E 是边长为 1 的正方形 ABCD 的对角线 BD 上的一个动点（不与 B、D 两点重合），过点 E 作直线 MN∥DC，交 AD 于 M，交 BC 于 N，连接 AE，作 EF⊥AE 于 E，交直线 CB 于 F．
（1）如图 1，当点 F 在线段 CB 上时，通过观察或测量，猜想△AEF 的形状，并证明你的猜想；
（2）如图 2，当点 F 在线段 CB 的延长线上时，其它条件不变，（1）中的结论还成立吗？若成立，请给出证明；若不成立，请说明理由；
（3）在点 E 从点D 向点B 的运动过程中，四边形 AFNM 的面积是否会发生变化？若发生了变化，请说明理由；若没有发生变化，请求出其面积的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图，平行四边形ABCD对角线AC、BD交于点O，∠ADB=20°，∠ACB=50°，过点O的直线交AD于点E，交BC于点F当点E从点A向点D移动过程中（点E与点A、点D不重合），四边形AFCE的形状变化依次是（ ）
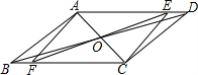
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→矩形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．
（1）将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；
（3）判断以O，A1，B为顶点的三角形的形状．（无须说明理由）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
