
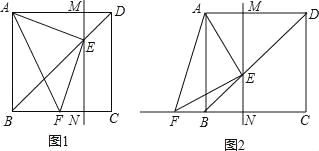
【题目】如图,点 E 是边长为 1 的正方形 ABCD 的对角线 BD 上的一个动点(不与 B、D 两点重合),过点 E 作直线 MN∥DC,交 AD 于 M,交 BC 于 N,连接 AE,作 EF⊥AE 于 E,交直线 CB 于 F.
(1)如图 1,当点 F 在线段 CB 上时,通过观察或测量,猜想△AEF 的形状,并证明你的猜想;
(2)如图 2,当点 F 在线段 CB 的延长线上时,其它条件不变,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由;
(3)在点 E 从点D 向点B 的运动过程中,四边形 AFNM 的面积是否会发生变化?若发生了变化,请说明理由;若没有发生变化,请求出其面积的值.
【答案】(1)△AEF是等腰直角三角形,证明见解析;(2)△AEF是等腰直角三角形,证明见解析;(3)四边形 AFNM 的面积没有发生改变,都是![]() .
.
【解析】
![]() 根据四边形 ABCD 是正方形,BD 是对角线,且 MN∥BA,求证△
根据四边形 ABCD 是正方形,BD 是对角线,且 MN∥BA,求证△
DEM 和△BNE 都是等腰直角三角形.又利用 EF⊥AE,可得∠EFN=∠AEM,然后即可求证,△AME≌△ENF;
![]() 利用(1)中证法求出 BN=EN=AM,∠AEM=∠EFN,即可得出答案;
利用(1)中证法求出 BN=EN=AM,∠AEM=∠EFN,即可得出答案;
![]() 分两种情况进行讨论:(i)当点 E 运动到 BD 的中点时,利用四边形 AFNM
分两种情况进行讨论:(i)当点 E 运动到 BD 的中点时,利用四边形 AFNM
是矩形,可得 S四边形AFNM=![]()
(ii)当点 E 不在 BD 的中点时,点 E 在运动(与点 B、D 不重合)的过程中,四边形 AFNM 是直角梯形.由(1)知,△AME≌△ENF,同理,图(2)△AME≌△ENF,然后即可得出结论.
(1)∵四边形 ABCD 是正方形,BD 是对角线,且 MN∥AB,
∴四边形 ABNM 和四边形 MNCD 都是矩形,
△NEB 和△MDE 都是等腰直角三角形.
∴∠AEF=∠ENF=90°,MN=BC=AB,EN=BN
![]()
即 EN=AM,
又∵∠AEM+∠FEN=90°,∠AEM+∠EAM=90°
∴∠EAM=∠FEN,
∵∠AME=∠ENF=90°,
∴△AME≌△ENF(ASA);
∴AE=BE,
∵AE⊥EF,
∴△AEF 是等腰直角三角形;
(2)由(1)同理可得:
∴BN=EN=AM,
∠AEM=∠EFN,
∵∠AME=∠ENF=90°
∴△AME≌△ENF(ASA);
∴AE=EF,
∵AE⊥EF,
∴△AEF 是等腰直角三角形;
四边形 AFNM 的面积没有发生变化
(i)当点 E 运动到 BD 的中点时,
四边形 AFNM 是矩形,S 四边形AFNM=![]()
(ii)当点 E 不在 BD 的中点时,点 E 在运动(与点 B、D 不重合)的过程中,四边形 AFNM 是直角梯形.
由(1)知,△AME≌△ENF,
同理,图(2),△AME≌△ENF,
∴FN=EM=DM.
∴FN+AM=DM+AM=AD=1
这时,S 四边形AFNM![]()
综合(i)、(ii)可知四边形 AFNM 的面积没有发生改变,都是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知 AB 是⊙O 的直径,点 C、D 在⊙O 上,过 D 点作 PF∥AC交⊙O 于 F,交 AB 于点 E,∠BPF=∠ADC
(1)求证:AEEB=DEEF.
(2)求证:BP 是⊙O 的切线:
(3)当的半径为![]() ,AC=2,BE=1 时,求 BP 的长,
,AC=2,BE=1 时,求 BP 的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC=BC,点D是BC上一点,∠ADE=∠C.
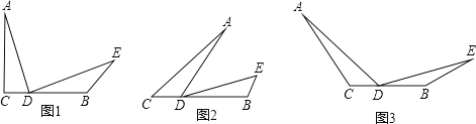
(1)如图1,若∠C=90°,∠DBE=135°.
①求证:∠EDB=∠CAD;
②求证:DA=DE;
(2)如图2,若∠C=40°,DA=DE,求∠DBE的度数;
(3)如图3,请直接写出∠DBE与∠C之间满足什么数量关系时,总有DA=DE成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
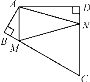
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副普通扑克牌中的4张;黑桃2,红心3,梅花4,黑桃5,洗匀后正面朝下放在桌面上.
(1)从中随机抽取一张牌是黑桃的概率是多少?
(2)从中随机抽取一张,再从剩下的牌中随机抽取另一张. 请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽取的两张牌牌面数字之和大于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念。
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
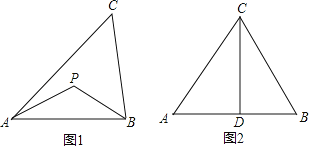
举例:如图1,若PA=PB,则点P为△ABC的准外心。
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=![]() AB,求∠APB的度数。
AB,求∠APB的度数。
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com