
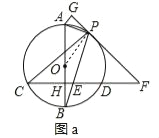
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB������ΪH��PΪ��AD��һ�㣬����PA��PB��PB��CD��E��
��1����ͼ��1������PC��CB����֤����BCP=��PED��
��2����ͼ��2������P����O�����߽�CD���ӳ����ڵ�E������A��PF�����ߣ�����ΪG����֤����APG=![]() ��F��
��F��
��3����ͼ��3����ͼ��2���������£�����PH����PH=PF��3PF=5PG��BE=2![]() �����O��ֱ��AB��
�����O��ֱ��AB��

���𰸡���1������������2������������3��AB=15
��������
��1���ɴ��������ó���CPB=��BCD�����ݡ�BCP=��BCD+��PCD=��CPB+��PCD=��PED���ɵ�֤��
��2������OP��֪OP=OB����֤��FPE=��FEP�á�F+2��FPE=180�㣬���ɡ�APG+��FPE=90��2��APG+2��FPE=180�㣬�ݴ˿ɵ�2��APG=��F���ݴ˼��ɵ�֤��
��3������AE��ȡAE�е�N������HN��PN������E��EM��PF����֤��PAE=��F����tan��PAE=tan��F��![]() ����֤��GAP=��MPE����sin��GAP=sin��MPE��
����֤��GAP=��MPE����sin��GAP=sin��MPE��![]() ���Ӷ��ó�
���Ӷ��ó�![]() ����MF=GP����3PF=5PG��
����MF=GP����3PF=5PG��![]() ������PG=3k����PF=5k��MF=PG=3k��PM=2k���ɡ�FPE=��PEF֪PF=EF=5k��EM=4k��PE=2
������PG=3k����PF=5k��MF=PG=3k��PM=2k���ɡ�FPE=��PEF֪PF=EF=5k��EM=4k��PE=2![]() k��AP=
k��AP=![]() k��֤��PEM=��ABP��BP=3
k��֤��PEM=��ABP��BP=3![]() k���̶��ɵ�BE=
k���̶��ɵ�BE=![]() k=2���ݴ����k=2���Ӷ��ó�AP��BP�ij������ù��ɶ����ɵô𰸣�
k=2���ݴ����k=2���Ӷ��ó�AP��BP�ij������ù��ɶ����ɵô𰸣�
֤������1����AB�ǡ�O��ֱ����AB��CD��
���CPB=��BCD��
���BCP=��BCD+��PCD=��CPB+��PCD=��PED��
���BCP=��PED��
��2������OP����OP=OB��
���OPB=��OBP��
��PF�ǡ�O�����ߣ�
��OP��PF�����OPF=90�㣬
��FPE=90�㩁��OPE��
�ߡ�PEF=��HEB=90�㩁��OBP��
���FPE=��FEP��
��AB�ǡ�O��ֱ����
���APB=90�㣬
���APG+��FPE=90�㣬
��2��APG+2��FPE=180�㣬
�ߡ�F+��FPE+��PEF=180�㣬
�ߡ�F+2��FPE=180��
��2��APG=��F��
���APG=![]() ��F��
��F��
��3������AE��ȡAE�е�N������HN��PN������E��EM��PF��M��
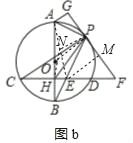
�ɣ�2��֪��APB=��AHE=90�㣬
��AN=EN��
��A��H��E��P�ĵ㹲Բ��
���PAE=��PHF��
��PH=PF��
���PHF=��F��
���PAE=��F��
tan��PAE=tan��F��
��![]() ��
��
�ɣ�2��֪��APB=��G=��PME=90�㣬
���GAP=��MPE��
��sin��GAP=sin��MPE��
��![]() ��
��
��![]() ��
��
��MF=GP��
��3PF=5PG��
��![]() ��
��
��PG=3k����PF=5k��MF=PG=3k��PM=2k
�ɣ�2��֪��FPE=��PEF��
��PF=EF=5k��
��EM=4k��
��tan��PEM=![]() ��tan��F=
��tan��F=![]() ��
��
��tan��PAE=![]() ��
��
��PE=![]() ��
��
��AP=![]() k��
k��
�ߡ�APG+��EPM=��EPM+��PEM=90�㣬
���APG=��PEM��
�ߡ�APG+��OPA=��ABP+��BAP=90�����ҡ�OAP=��OPA��
���APG=��ABP��
���PEM=��ABP��
��tan��ABP=tan��PEM����![]() ��
��
��![]() ��
��
��BP=3![]() k��
k��
��BE=![]() k=2
k=2![]() ��
��
��k=2��
��AP=3![]() ��BP=6
��BP=6![]() ��
��
���ݹ��ɶ����ã�AB=15��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬�ԡ�ABC��һ��Ϊ�����������Σ�ʹ�����ĵ����������ڡ�ABC���������ϣ�����Ի����IJ�ͬ�ĵ��������εĸ������Ϊ_____��
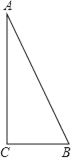
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��10��13�����磬2019��֣�����б���֣�ݹ�������������֣������CBD���������ǹ����������ı���������ȫ�̡���������ɺͽ����ܡ���ͥ���ĸ��������������ȫ��32�����Һ͵�����2.6����ѡ�ֲμӱ��������Ӱ�̱����У��й�ѡ�����������ܺ�һֱ��������ǰ������̽�ͻȻ���٣���1Сʱ09��21��ijɼ�������Ӱ�̹ھ��������ܹ���ӳ�������ڱ���;���ٶ�v��ʱ��t֮��ĺ�����ϵ�Ĵ���ͼ���ǣ� ��
A.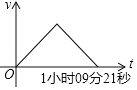 B.
B.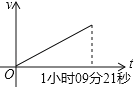
C.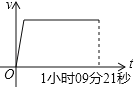 D.
D.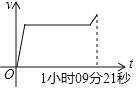
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
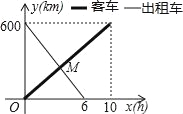
����Ŀ��һ���ͳ��Ӽؿ����ҵأ�һ��������ҵؿ����أ�����ͬʱ������������ص�·��y��km����ͳ���ʻʱ��x��h����ĺ�����ϵ��ͼ��������Ϣ��
��1��������ٶ�Ϊ100ǧ��/ʱ��
��2���ͳ����ٶ�Ϊ60ǧ��/ʱ��
��3����������ʱ���ͳ���ʻ��3.75Сʱ��
��4������ʱ�������ص�·��Ϊ225ǧ�ף�
������ȷ�ĸ����У�������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������ABC��AB��AC��AD����ABC�Ľ�ƽ���ߣ�DE��AB��DF��AC������ֱ�ΪE��F���������ĸ������У���AB��һ����AC��һ�㵽D�ľ�����ȣ���AD������һ�㵽AB��AC�ľ�����ȣ��ۡ�BDE����CDF����BD=CD��AD��BC��������ȷ�ĸ�����
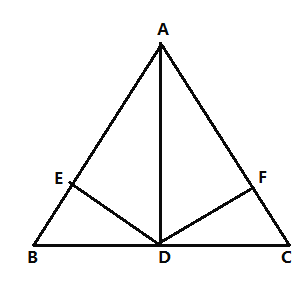
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC��������������ֱ���A��1��1����B��4��1����C��3��3����
��1������ABC����ƽ��5����λ��õ���A1B1C1���뻭����A1B1C1��
��2������ABC��ԭ��O��ʱ����ת90����õ���A2B2C2���뻭����A2B2C2��
��3���ж���O��A1��BΪ����������ε���״��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AO��CO��BO��DO������ABC����ADC��180��
(1) ��֤���ı���ABCD�Ǿ���
(2) ��DE��AC��BC��E����ADB�á�CDB��2��3������BDE�Ķ����Ƕ��٣�
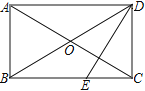
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���BAC=45�㣬CD��AB������Ϊ��D��MΪ�߶�DB��һ���㣨�������˵㣩����N��ֱ��AC���Ϸ��ҡ�NCM=135�㣬CN=CM����ͼ�٣�
��1����֤����ACN=��AMC��
��2���ǡ�ANC�����Ϊ5���ǡ�ABC�����Ϊ5����֤��![]() ��
��
��3���ӳ��߶�AB����P��ʹBP=BM����ͼ�ڣ�̽���߶�AC���߶�DB����ʲô������ϵʱ�������������������M��AN=CPʼ�ճ�������д��̽�����̣�
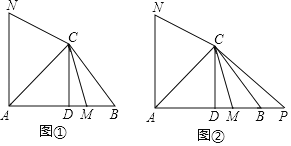
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com