
【题目】阅读下列 材料,并解答总题:
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母x+1,可设![]()
则![]()
=![]()
∵对于任意![]() 上述等式成立
上述等式成立
∴![]() ,
,
解得![]() ,
,
∴![]()
这样,分式![]() 就拆分成一个整式
就拆分成一个整式![]() 与一个分式
与一个分式![]() 的和的形式.
的和的形式.
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式为___________;
拆分成一个整式与一个分式(分子为整数)的和的形式为___________;
(2)已知整数![]() 使分式
使分式![]() 的值为整数,则满足条件的整数
的值为整数,则满足条件的整数![]() =________.
=________.
【答案】(1)![]() ;(2)4、16、2、-10
;(2)4、16、2、-10
【解析】
(1)仿照例题,列出方程组,求出a、b的值,把原式拆分成一个整式与一个分式(分子为整数)的和的形式;
(2)仿照例题,列出方程组,求出a、b的值,把原式拆分成一个整式与一个分式(分子为整数)的和的形式,根据整除运算解答;
解:(1)由分母x-1,可设x2+6x-3=(x-1)(x+a)+b
则x2+6x-3=(x-1)(x+a)+b=x2+ax-x-a+b=x2+(a-1)x-a+b
∵对于任意x上述等式成立,
![]()
解得:![]() ,
,
![]() 拆分成x+7+
拆分成x+7+![]()
故答案为:x+7+![]()
(2)由分母x-3,可设2x2+5x-20=(x-3)(2x+a)+b
则2x2+5x-20=(x-3)(2x+a)+b=2x2+ax-6x-3a+b=2x2+(a-6)x-3a+b
∵对于任意x上述等式成立,
![]() ,解得
,解得![]()
![]() 拆分成2x+11+
拆分成2x+11+![]()
∵整数![]() 使分式
使分式![]() 的值为整数,
的值为整数,
∴![]() 为整数,
为整数,
则满足条件的整数x=4、16、2、-10,
故答案为:4、16、2、-10;


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
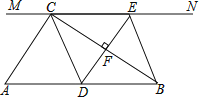
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由.
(2)在(1)的条件下,当∠A=__________°时,四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
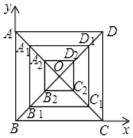
【题目】如图以正方形ABCD的B点为坐标原点.BC所在直线为x轴,BA所在直线为y轴,建立直角坐标系.设正方形ABCD的边长为6,顺次连接OA、OB、OC、OD的中点A1、B1、C1、D1,得到正方形A1B1C1D1,再顺次连接OA1、OB1、OC1、OD1的中点得到正方形A2B2C2D2.按以上方法依次得到正方形A1B1C1D1,……AnBnCnDn,(n为不小于1的自然数),设An点的坐标为(xn,yn),则xn+yn=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD 分别为两圆的弦,AC、BD 为两圆的公切线且相交于点 P.若 PC=2,DB=6,∠APB=90°.
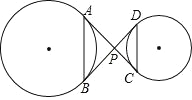
(1)求△PAB 的周长.
(2)求△PAB 与△PCD 的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:已知二次函数的图象与![]() 轴交于
轴交于![]() 和
和![]() 两点.交
两点.交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,![]() 是二次函数图象上的一对对称点,一次函数的图象过点
是二次函数图象上的一对对称点,一次函数的图象过点![]() ,
,![]()
(1)画出图象,并求二次函数的解析式.
(2)根据图象直接写出使一次函数值大于或等于二次函数值的![]() 的取值范围.
的取值范围.
(3)若直线与![]() 轴交点为
轴交点为![]() ,连接
,连接![]() ,
,![]() ,求三角形
,求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
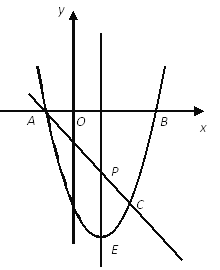
【题目】如图,抛物线![]() 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B、C的坐标分别为:A(﹣2,1),B(﹣3,﹣1),C(1,﹣1).若以A,B,C,D为顶点的四边形为平行四边形,那么点D的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com