练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°，顶部的仰角为37°，已知教学楼和实验楼在同一平面上，观测点距地面的垂直高度AB为15m，求实验楼的垂直高度即CD长（精确到1m）．

    参考值：sin37°=0.60，cos37°=0.80，tan37°=0.75．

    【答案】26．

    【解析】试题分析：作AE⊥CD于E，根据正切的定义求出CE和AE，计算即可．

    试题解析：解：作AE⊥CD于E，∵AB=15m，∴DE=AB=15m，∵∠DAE=45°，∴AE=DE=15m，在Rt△ACE中，tan∠CAE=，则CE=AEtan37°=15×0.75≈11cm，∴AB=CE+DE=11+15=26m．

    答：实验楼的垂直高度即CD长为26m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在五边形ADBCE中，∠ADB=∠AEC=90°，∠DAB=∠EAC，M、N、O分别为AC、AB、BC的中点．

    （1）求证：△EMO≌△OND；

    （2）若AB=AC，且∠BAC=40°，当∠DAB等于多少时，四边形ADOE是菱形，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店购进一批童装，每件售价120元，可获利20%，这件童装的进价是_____元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点E、F分别在平行四边形ABCD的边BC、AD上，BE=DF，点P在边AB上，AP：PB=1：n（n＞1），过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分，将△CDF分成面积为S3、S4的两部分（如图），下列四个等式：

    ①

    ②

    ③

    ④

    其中成立的有（　　）

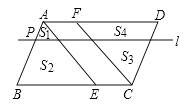
    A. ①②④ B. ②③ C. ②③④ D. ③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线BC//OA,∠C=∠OAB=100°,E，F在CB上，且满足∠FOB=∠AOB,OE平分∠COF.

    (1)求∠BOE的度数；

    (2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围；若不变，求出这个比值（提示:图中∠OFC=∠BOF+∠OBC）；

    (3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出∠OEC度数；若不存在,说明理由(提示：三角形三个内角的和为180）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校5月份举行了八年级生物实验考查，有A和B两个考查实验，规定每位学生只参加其中一个实验的考查，并由学生自己抽签决定具体的考查实验，小明、小丽、小华都参加了本次考查．

    （1）小丽参加实验A考查的概率是 ；

    （2）用列表或画树状图的方法求小明、小丽都参加实验A考查的概率；

    （3）他们三人都参加实验A考查的概率是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为迎接“均衡教育大检查”，县委县府对通往某偏远学校的一段全长为1200 米的道路进行了改造，铺设草油路面．铺设400 米后，为了尽快完成道路改造，后来每天的工作效率比原计划提高25%，结果共用13天完成道路改造任务．

    （1）求原计划每天铺设路面多少米；

    （2）若承包商原来每天支付工人工资为1500元，提高工作效率后每天支付给工人的工资增长了20%，完成整个工程后承包商共支付工人工资多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读理解下面的例题，再按要求解答下列问题：

    例题：求代数式y2+4y+8的最小值．

    解：y2+4y+8=y2+4y+4+4=（y+2）2+4

    ∵（y+2）2≥0

    ∴（y+2）2+4≥4

    ∴y2+4y+8的最小值是4．

    （1）求代数式m2+m+4的最小值；

    （2）求代数式4﹣x2+2x的最大值；

    （3）某居民小区要在一块一边靠墙（墙长15m）的空地上建一个长方形花园ABCD，花园一边靠墙，另三边用总长为20m的栅栏围成．如图，设AB=x（m），请问：当x取何值时，花园的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

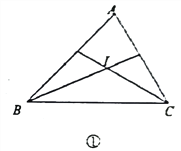
    【题目】如图①，△ABC中，∠ABC与∠ACB的平分线交于点I.根据下列条件，求∠BIC的

    度数。

    （1）若∠ABC=60°，∠ACB=70°,则∠BIC=

    （2）若∠ABC+∠ACB=130°，则∠BIC=

    （3）若∠A=50°，则∠BIC=

    （4）若∠A=110°，则∠BIC=

    （5）从上述计算中，我们能发现已知∠A，求∠BIC的公式是：∠BIC= .

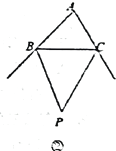
    （6）如图②，BP，CP分别是∠ABC与∠ACB的外角平分线，交于点P.

    若已知∠A，则求∠BPC的公式是：∠BPC=

    查看答案和解析>>

    同步练习册答案