
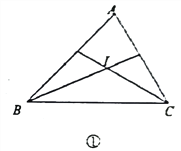
【题目】如图①,△ABC中,∠ABC与∠ACB的平分线交于点I.根据下列条件,求∠BIC的
度数。
(1)若∠ABC=60°,∠ACB=70°,则∠BIC=
(2)若∠ABC+∠ACB=130°,则∠BIC=
(3)若∠A=50°,则∠BIC=
(4)若∠A=110°,则∠BIC=
(5)从上述计算中,我们能发现已知∠A,求∠BIC的公式是:∠BIC= .
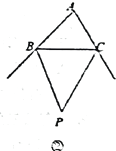
(6)如图②,BP,CP分别是∠ABC与∠ACB的外角平分线,交于点P.
若已知∠A,则求∠BPC的公式是:∠BPC=
【答案】(1)115°;(2)115°;(3)115°(4)145°(5)90°+![]() ∠A:(6)90°-
∠A:(6)90°-![]() ∠A.
∠A.
【解析】试题分析:根据角平分线的定义和三角形的内角和定理求解即可.
试题解析:解:(1)∵BI是∠ABC的平分线,∠ABC=60°,∴∠CBI=![]() ∠ABC=30°.
∠ABC=30°.
∵CI是∠ACB的平分线,∠ACB=70°,∴∠BCI=![]() ∠ACB=35°.
∠ACB=35°.
在△BCI中,∵∠BIC+∠BCI+∠CBI=180°,∴∠BIC=180°﹣30°﹣35°=115°;
(2)∵BI是∠ABC的平分线,CI是∠ACB的平分线,∴∠CBI=![]() ∠ABC,∠BCI=
∠ABC,∠BCI=![]() ∠ACB,∴∠CBI+∠BCI=
∠ACB,∴∠CBI+∠BCI=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°=65°.
×130°=65°.
在△BCI中,∵∠BIC+∠BCI+∠CBI=180°,∴∠BIC=180°﹣65°=115°;
(3)在△ABC中,∵∠A+∠ABC+∠ACB=180°,∠A=50°,∴∠ABC+∠ACB=180°﹣∠A=130°.
∵BI是∠ABC的平分线,CI是∠ACB的平分线,∴∠CBI=![]() ∠ABC,∠BCI=
∠ABC,∠BCI=![]() ∠ACB,
∠ACB,
∴∠CBI+∠BCI=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°=65°.
×130°=65°.
在△BCI中,∵∠BIC+∠BCI+∠CBI=180°,∴∠BIC=180°﹣65°=115°;
(4)在△ABC中,∵∠A+∠ABC+∠ACB=180°,∠A=110°,∴∠ABC+∠ACB=180°﹣∠A=70°.∵BI是∠ABC的平分线,CI是∠ACB的平分线,∴∠CBI=![]() ∠ABC,∠BCI=
∠ABC,∠BCI=![]() ∠ACB,∴∠CBI+∠BCI=
∠ACB,∴∠CBI+∠BCI=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×70°=35°.
×70°=35°.
在△BCI中,∵∠BIC+∠BCI+∠CBI=180°,∴∠BIC=180°﹣35°=145°;
(5)在△ABC中,∵∠A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=180°﹣∠A.
∵BI是∠ABC的平分线,CI是∠ACB的平分线,∴∠CBI=![]() ∠ABC,∠BCI=
∠ABC,∠BCI=![]() ∠ACB,
∠ACB,
∴∠CBI+∠BCI=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×(180°﹣∠A)=90°﹣
×(180°﹣∠A)=90°﹣![]() ∠A.
∠A.
在△BCI中,∵∠BIC+∠BCI+∠CBI=180°,∴∠BIC=180°﹣(90°﹣![]() ∠A)=90°+
∠A)=90°+![]() ∠A;
∠A;
(6)∵∠CBD,∠BCE是△ABC的外角,∴∠CBD=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠CBD+∠BCE=∠A+∠ACB+∠A+∠ABC=180°+∠A.
∵BP,CP分别是∠ABC与∠ACB的外角平分线,∴∠CBP=![]() ∠CBD,∠BCP=
∠CBD,∠BCP=![]() ∠BCE
∠BCE
∴∠CBP+∠BCP=![]() (∠CBD+∠BCE)=
(∠CBD+∠BCE)=![]() (180°+∠A)=90°+
(180°+∠A)=90°+![]() ∠A.
∠A.
在△BCP中,∵∠BCP+∠CBP+∠BPC=180,∴∠BPC=180°﹣(90°+![]() ∠A)=90°﹣
∠A)=90°﹣![]() ∠A.
∠A.


科目:初中数学 来源: 题型:
【题目】如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m).
参考值:sin37°=0.60,cos37°=0.80,tan37°=0.75.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国网民已达到731 000 000人,用科学记数法表示为( )人
A. 0.731×109 B. 7.31×108 C. 7.31×109 D. 73.1×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为带分数.例如: ![]() =2+
=2+![]() =2
=2![]() 在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如: ![]() 这样的分式就是假分式;
这样的分式就是假分式; ![]() 这样的分式就是真分式 .类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
这样的分式就是真分式 .类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
例如: ![]() =
=![]() =1-
=1-![]() =
=![]() =
=![]() =
= ![]()
![]()
(1)将分式![]() 化为带分式;
化为带分式;
(2)若分式![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为![]() 元,则可卖出(350-10
元,则可卖出(350-10![]() )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
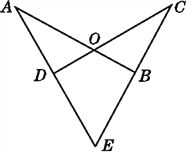
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,且∠1=20°,∠2=45°+α,∠3=60°-α,∠4=40°-α,∠5=30°.则α的值为( )
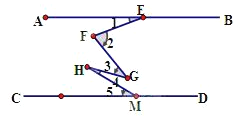
A. 10° B. 15° C. 20° D. 25°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com