【题目】某商店从厂家以21元的价格购进一批商品，该商品可以自行定价，若每件商品售价为
元，则可卖出（350－10）件，但物价局限定每件商品加价不能超过进价的20%，商店计划要赚400元，需要卖出多少件商品?每件商品应售多少元？
金钥匙试卷系列答案科目：初中数学 来源： 题型：
【题目】如图，直线BC//OA,∠C=∠OAB=100°,E，F在CB上，且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE的度数；
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围；若不变，求出这个比值（提示:图中∠OFC=∠BOF+∠OBC）；
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出∠OEC度数；若不存在,说明理由(提示：三角形三个内角的和为180）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】中国人很早就开始使用负数，中国古代数学著作《九章算术》．如果收入120元记作+120元，那么-100元表示( )
A.支出20元B.支出100元C.收入20元D.收入100元
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校想知道九年级学生对我国倡导的“一带一路”的了解程度，随机抽取部分九年级学生进行问卷调查，问卷设有4个选项（每位被调查的学生必选且只选一项）：A．非常了解．B．了解．C．知道一点．D．完全不知道．将调查的结果绘制如下两幅不完整的统计图，请根据两幅统计图中的信息，解答下列问题：
（1）求本次共调查了多少学生？
（2）补全条形统计图；
（3）该校九年级共有600名学生，请你估计“了解”的学生约有多少名？
（4）在“非常了解”的3人中，有2名女生，1名男生，老师想从这3人中任选两人做宣传员，请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
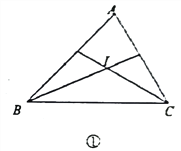
【题目】如图①，△ABC中，∠ABC与∠ACB的平分线交于点I.根据下列条件，求∠BIC的
度数。
（1）若∠ABC=60°，∠ACB=70°,则∠BIC=
（2）若∠ABC+∠ACB=130°，则∠BIC=
（3）若∠A=50°，则∠BIC=
（4）若∠A=110°，则∠BIC=
（5）从上述计算中，我们能发现已知∠A，求∠BIC的公式是：∠BIC= .
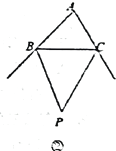
（6）如图②，BP，CP分别是∠ABC与∠ACB的外角平分线，交于点P.
若已知∠A，则求∠BPC的公式是：∠BPC=
查看答案和解析>>
科目：初中数学 来源： 题型：
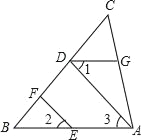
【题目】如图，已知点D、F、E、G都在△ABC的边上，EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度数．（请在下面的空格处填写理由或数学式）
解：∵EF∥AD，（已知）
∴∠2= （ ）
∵∠1=∠2，（已知）
∴∠1= （ ）
∴ ∥ ，（ ）
∴∠AGD+ =180°，（两直线平行，同旁内角互补）
∵ ，（已知）
∴∠AGD= （等式性质）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线
，直线
与直线
、
分别相交于C、D两点．
（1）如图a，有一动点P在线段CD之间运动(不与C、D两点重合)，问在点P的运动过程中，是否始终具有∠3+∠1=∠2这一关系，为什么？
（2）如图b，当动点P线段CD之外运动(不与C、D两点重合)，问上述结论是否成立?若不成立，试写出新的结论并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
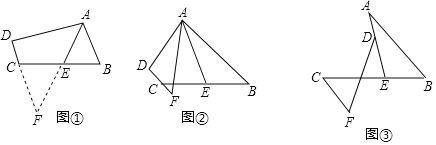
【题目】（1）阅读理解：如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系．
解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC，得到AB=FC，从而把AB，AD，DC转化在一个三角形中即可判断．
AB、AD、DC之间的等量关系为 ；
（2）问题探究：如图②，在四边形ABCD中，AB∥DC，AF与DC的延长线交于点F，E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论．
（3）问题解决：如图③，AB∥CF，AE与BC交于点E，BE：EC=2：3，点D在线段AE上，且∠EDF=∠BAE，试判断AB、DF、CF之间的数量关系，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
