Question

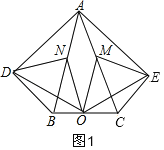
【题目】在五边形ADBCE中，∠ADB=∠AEC=90°，∠DAB=∠EAC，M、N、O分别为AC、AB、BC的中点．

（1）求证：△EMO≌△OND；

（2）若AB=AC，且∠BAC=40°，当∠DAB等于多少时，四边形ADOE是菱形，并证明．

Answer 1

【答案】（1）证明见解析（2）当∠DAB等于35°时，四边形ADOE是菱形

【解析】试题分析：（1）根据直角三角形斜边中线等于斜边一半得：DN=AB，由中位线定理得：OM=AB，则OM=DN，同理得：ON=ME，再根据外角定理和已知证明其夹角相等，则两三角形全等；

（2）连接AO，当∠DAB等于35°时，四边形ADOE是菱形，如图2，设∠DAB=x°，则∠BND=2x°，易证得OD=OE，AD=AE，因此只要AD=OD，四边形ADOE就是菱形；即∠DAO=∠AOD，列关于x的方程解出即可．

试题解析：证明：（1）∵∠ADB=90°，N是AB的中点，∴DN=AB=AN，∴∠ADN=∠BAD，∵O是AB的中点，M是AC的中点，∴OM是△ABC的中位线，∴OM=AB，OM∥AB，∴∠OMC=∠BAC，同理得：∠BNO=∠BAC，∴∠BNO=∠OMC，∵DN=AB，OM=AB，∴DN=OM，同理得：ME=ON，∵∠BND=∠ADN+∠BAD，∠CME=∠CAE+∠AEM，∴∠BND=2∠BAD，∠CME=2∠CAE，∵∠BAD=∠CAE，∴∠BND=∠CME，∴∠BND+∠BNO=∠CME+∠OMC，即∠DNO=∠EMO，∴△EMO≌△OND；

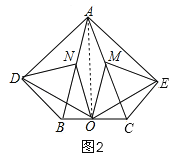
（2）当∠DAB等于35°时，四边形ADOE是菱形，理由是：

如图2，连接AO，设∠DAB=x°，则∠BND=2x°，∵AB=AC，O是BC的中点，∴AO平分∠BAC，AO⊥BC，∵∠BAC=40°，∴∠BAO=20°，在Rt△ABO中，N是AB的中点，∴ON=AB=AN，∴∠BAO=∠AON=20°，∴∠BNO=40°，由（1）得：ON=AC，DN=AB，∴ON=DN，∴∠NDO=∠NOD=（180°-∠DNO）=90°﹣（2x°+40°）=70°﹣x°，∵∠ADB=∠AEC=90°，∠BAD=∠CAE，AB=AC，∴△ADB≌△AEC，∴AD=AE，由（1）得：△EMO≌△OND，∴OD=OE，∴当AD=OD时，四边形ADOE是菱形，即∠DAO=∠AOD，x+20=70﹣x+20，x=35，∴当∠DAB等于35°时，四边形ADOE是菱形．