【题目】如图，AB∥CD，∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H，∠K﹣∠H=27°，则∠K=（ ）
A. 76° B. 78° C. 80° D. 82°
【答案】B
【解析】如图，分别过K、H作AB的平行线MN和RS，
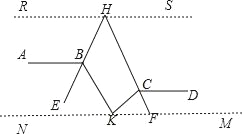
∵AB∥CD，
∴AB∥CD∥RS∥MN，
∴∠RHB=∠ABE=
∠ABK，∠SHC=∠DCF=∠DCK，∠NKB+∠ABK=∠MKC+∠DCK=180°，
∴∠BHC=180°﹣∠RHB﹣∠SHC=180°﹣（∠ABK+∠DCK），
∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣（180°﹣∠ABK）﹣（180°﹣∠DCK）=∠ABK+∠DCK﹣180°，
∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC，
又∠BKC﹣∠BHC=27°，
∴∠BHC=∠BKC﹣27°，
∴∠BKC=180°﹣2（∠BKC﹣27°），
∴∠BKC=78°，
故选：B．
科目：初中数学 来源： 题型：
【题目】大源村在“山上再造一个通城”工作中，计划植树200亩，全村在完成植树40亩后，党的群众路线教育实践活动工作小组加入村民植树活动，并且该活动小组植树的速度是全村植树速度的1.5倍，整个植树过程共用了13天完成．
（1）全村每天植树多少亩？
（2）如果全村植树每天需2000元工钱，党的群众路线教育实践活动工作小组是义务植树，因此实际工钱比计划节约多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，△ ABC ≌△ ADE ，延长 BC 分别交 AD ， DE 于 F ， G ，∠ CAD ＝10°，∠ B ＝∠ D ＝25°，∠ EAB ＝120°.求∠ DFB 和∠ DGB 的度数．
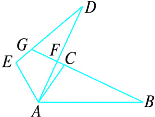
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB⊥BC，BC⊥CD，∠1=∠2．试判断BE与CF的关系，并说明你的理由．
解：BE∥CF．
理由：∵AB⊥BC，BC⊥CD（已知）
∴∠ =∠ =90°（ ）
∵∠1=∠2（ ）
∴∠ABC﹣∠1=∠BCD﹣∠2，即∠EBC=∠BCF.
∴ ∥ ．（____________,______________）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AM∥BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．
（1）求∠CBD的度数；
（2）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．
（3）当点P运动到使∠ACB=∠ABD时，∠ABC的度数是 ．
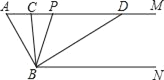
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在五边形ADBCE中，∠ADB=∠AEC=90°，∠DAB=∠EAC，M、N、O分别为AC、AB、BC的中点．
（1）求证：△EMO≌△OND；
（2）若AB=AC，且∠BAC=40°，当∠DAB等于多少时，四边形ADOE是菱形，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
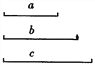
【题目】作图题： （1）已知：如图，线段a、b、c．
求作：ΔABC，使得BC＝a，AC＝b，AB＝c．（保留作图痕迹，不写作法）
（2）求作：∠AOB的平分线OC.（不写作法，保留作图痕迹）
查看答案和解析>>
科目：初中数学 来源： 题型：
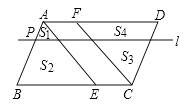
【题目】点E、F分别在平行四边形ABCD的边BC、AD上，BE=DF，点P在边AB上，AP：PB=1：n（n＞1），过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分，将△CDF分成面积为S3、S4的两部分（如图），下列四个等式：
①
②
③
④
其中成立的有（ ）
A. ①②④ B. ②③ C. ②③④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com