
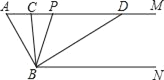
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
【答案】(1)60°;(2)不变化,∠APB=2∠ADB,证明详见解析;(3)30°.
【解析】试题分析:(1)已知AM∥BN,根据两直线平行,同旁内角互补可得∠A+∠ABN=180°,从而求得ABN=120°;已知BC、BD分别平分∠ABP和∠PBN,根据角平分线的定义可得∠CBP=![]() ∠ABP,∠DBP=
∠ABP,∠DBP=![]() ∠NBP,所以∠CBD=
∠NBP,所以∠CBD=![]() ∠ABN=60°;(2)不变化,∠APB=2∠ADB,已知AM∥BN,根据两直线平行,内错角相等即可得∠APB=∠PBN,∠ADB=∠DBN;由BD平分∠PBN,根据角平分线的定义可得∠PBN=2∠DBN,即可得∠APB=2∠ADB;(3)由AD∥BN,根据两直线平行,内错角相等即可得∠ACB=∠CBN;又∠ACB=∠ABD,可得∠CBN=∠ABD,所以∠ABC=∠DBN;
∠ABN=60°;(2)不变化,∠APB=2∠ADB,已知AM∥BN,根据两直线平行,内错角相等即可得∠APB=∠PBN,∠ADB=∠DBN;由BD平分∠PBN,根据角平分线的定义可得∠PBN=2∠DBN,即可得∠APB=2∠ADB;(3)由AD∥BN,根据两直线平行,内错角相等即可得∠ACB=∠CBN;又∠ACB=∠ABD,可得∠CBN=∠ABD,所以∠ABC=∠DBN;
由(1)可得,∠CBD=60°,∠ABN=120°,即可求得∠ABC=![]() (120°﹣60°)=30°.
(120°﹣60°)=30°.
试题解析:
(1)∵AM∥BN,
∴∠A+∠ABN=180°,
∵∠A=60°,
∴∠ABN=120°,
∵BC、BD分别平分∠ABP和∠PBN,
∴∠CBP=![]() ∠ABP,∠DBP=
∠ABP,∠DBP=![]() ∠NBP,
∠NBP,
∴∠CBD=![]() ∠ABN=60°;
∠ABN=60°;
(2)不变化,∠APB=2∠ADB,
证明:∵AM∥BN,
∴∠APB=∠PBN,
∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AD∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠DBN,
由(1)可得,∠CBD=60°,∠ABN=120°,
∴∠ABC=![]() (120°﹣60°)=30°,
(120°﹣60°)=30°,
故答案为:30°.


科目:初中数学 来源: 题型:
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求![]() 的值;
的值;
(3)在(2)的条件下,若![]() =k(k为大于
=k(k为大于![]() 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,分别延长△ABC的边AB,AC到D,E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业时发现如下规律:
①若∠A=50°,则∠P=65°=90°-![]() ;
;
②若∠A=90°,则∠P=45°=90°-![]() ;
;
③若∠A=100°,则∠P=40°=90°-![]() .
.
(1)根据上述规律,若∠A=150°,则∠P=________;
(2)请你用数学表达式写出∠P与∠A的关系;
(3)请说明(2)中结论的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的有( )
①Rt△ABC中,已知两边长分别为3和4,则第三边长为5;
②有一个内角等于其他两个内角和的三角形是直角三角形;
③三角形的三边分别为a,b,C,若a2+c2=b2,那么∠C=90°;
④若△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店欲购进甲、乙两种新款运动服。甲款每套进价350元,乙款每套进价200元。该店计划用不低于7600元且不高于8000元的资金订购甲、乙两款运动服共30套
(1)该店订购这两款运动服,共有哪几种方案?
(2)若该店以甲款每套400元、乙款每套300元的价格全部售出,哪种方案获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com