
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

【答案】(1)∠ABE+∠CDE=∠BED;(2)详见解析;(3)2∠BFD+∠BED=360°.
【解析】试题分析:(1)点E作EF∥AB,根据平行线的性质易证得∠1=∠ABE,∠2=∠CDE,则可得∠ABE+∠CDE=∠BED;(2)∠BFD=![]() ∠BED,已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=
∠BED,已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,所以∠ABF+∠CDF=
∠CDE,所以∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),由(1)的结论可得∠BFD=∠ABF+∠CDF=
(∠ABE+∠CDE),由(1)的结论可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE),∠BED=∠ABE+∠CDE,所以∠BFD=
(∠ABE+∠CDE),∠BED=∠ABE+∠CDE,所以∠BFD=![]() ∠BED;(3过点E作EG∥CD,根据平行公理可得AB∥CD∥EG,根据平行线的性质易证∠ABE+∠CDE+∠BED=360°,再由(1)的方法可得∠BFD=∠ABF+∠CDF;已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=
∠BED;(3过点E作EG∥CD,根据平行公理可得AB∥CD∥EG,根据平行线的性质易证∠ABE+∠CDE+∠BED=360°,再由(1)的方法可得∠BFD=∠ABF+∠CDF;已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,所以∠BFD=
∠CDE,所以∠BFD=![]() (∠ABE+∠CDE),即2∠BFD+∠BED=360°.
(∠ABE+∠CDE),即2∠BFD+∠BED=360°.
试题解析:
(1)∠ABE+∠CDE=∠BED.
理由:如图1,作EF∥AB,
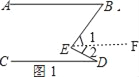
∵直线AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案为:∠ABE+∠CDE=∠BED.
(2)∠BFD=![]() ∠BED.
∠BED.
理由:如图2,∵BF,DF分别平分∠ABE,∠CDE,
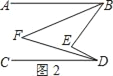
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
由(1),可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
(3)2∠BFD+∠BED=360°.
理由:如图3,过点E作EG∥CD,
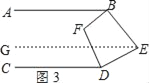
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案为:2∠BFD+∠BED=360°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1,
(x﹣1)(x2+x+1)=x3﹣1,
(x﹣1)(x3+x2+x+1)=x4﹣1,
……
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= .
(2)你能否由此归纳出一般性规律:(x﹣1)(xn+xn﹣1+…+x+1)= .
(3)根据以上规律求1+3+32+…+334+335的结果
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果把一个自然数各数位上数字从最高位到个位依次排出一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数叫做 “和谐数”.例如:自然数64746从最高位到个位排出的一串数字是:6、4、7、4、6,从个位到最高排出的一串数字也是:6、4、7、4、6,所64746是“和谐数”.再如:33,181,212,4664,…,都是“和谐数”.
(1)请你直接写出3个四位“和谐数”,猜想任意一个四位“和谐数”能否被11整除,并说明理由;[来。
(2) 已知一个能被11整除的三位“和谐数”,设个位上的数字为x(![]() ,x为自然数),十位上的数字为y,求y与x的函数关系式.
,x为自然数),十位上的数字为y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
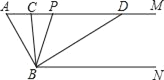
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市为方便相距2 km的A,B两处居民区的交往,修筑一条笔直的公路(即图中的线段AB),经测量,在A处的北偏东60°方向、B处北偏西45°方向的C处有一半径为0.7 km的圆形公园,问计划修筑的公路会不会穿过公园?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
(1)求证:△EMO≌△OND;
(2)若AB=AC,且∠BAC=40°,当∠DAB等于多少时,四边形ADOE是菱形,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生由于看错了运算符号,把一个整式A减去多项式ab-2bc+3ac误认为加上这个多项式,结果得出的答案是2bc-3ac+2ab.
(1)求整式A;
(2)求原题的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
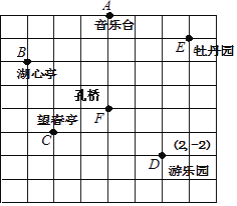
【题目】王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,﹣2),请你帮她画出坐标系,并写出其他各景点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BC//OA,∠C=∠OAB=100°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值(提示:图中∠OFC=∠BOF+∠OBC);
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出∠OEC度数;若不存在,说明理由(提示:三角形三个内角的和为180).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com