
【题目】如图,小明站在某广场一看台C处,从眼睛D处测得广场中心F的俯角为21°,若CD=1.6米,BC=1.5米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10米,则看台底端A点距离广场中心F点的距离约为(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)( )
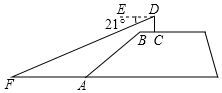
A.8.8米B.9.5米C.10.5米D.12米
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,某建筑物![]() 上挂着“巴山渝水,魅力重庆”的宣传条幅
上挂着“巴山渝水,魅力重庆”的宣传条幅![]() ,王同学利用测倾器在斜坡的底部
,王同学利用测倾器在斜坡的底部![]() 处测得条幅底部
处测得条幅底部![]() 的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡
的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡![]() 的坡度
的坡度![]() 米,
米,![]() 米(点
米(点![]() 在同平面内,
在同平面内,![]() ,测倾器的高度忽略不计),则条幅
,测倾器的高度忽略不计),则条幅![]() 的长度约为(参考数据:
的长度约为(参考数据:![]()
![]() )
)
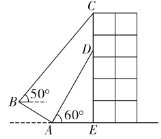
A.12.5米B.12.8米C.13.1米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,甲、乙两人在附近的景点游玩,甲从![]() 、
、![]() 、
、![]() 三个景点中任意选择一个游玩,乙从
三个景点中任意选择一个游玩,乙从![]() 、
、![]() 两个景点中任意选择一个游玩.
两个景点中任意选择一个游玩.
(1)乙恰好游玩![]() 景点的概率为 ;
景点的概率为 ;
(2)用列表或画树状图的方法列出所有等可能的结果.并求甲、乙恰好游玩同一景点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察猜想:
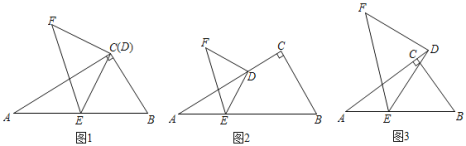
(1)如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D与点C重合,点E在斜边AB上,连接DE,且DE=AE,将线段DE绕点D顺时针旋转90°得到线段DF,连接EF,则![]() =______,sin∠ADE=________,
=______,sin∠ADE=________,
探究证明:
(2)在(1)中,如果将点D沿CA方向移动,使CD=![]() AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
拓展延伸
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=a,点D在边AC的延长线上,E是AB上任意一点,连接DE.ED=nAE,将线段DE绕着点D顺时针旋转90°至点F,连接EF.求![]() 和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)
和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲乙两种商品,甲的进货单价比乙的进货单价高20元,已知20个甲商品的进货总价与25个乙商品的进货总价相同.
(1)求甲、乙每个商品的进货单价;
(2)若甲、乙两种商品共进货100件,要求两种商品的进货总价不高于9000元,同时甲商品按进价提高10%后的价格销售,乙商品按进价提高25%后的价格销售,两种商品全部售完后的销售总额不低于10480元,问有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位正整数数m,若其千位与百位上的数字之和为9,十位与个位上的数字之和也为9,那么称m为“重九数”,如:1827、3663.将“重九数”m的千位数字与十位数字对调,百位数字与个位数字对调,得到一个新的四位正整数数n,如:m=2718,则n=1827,记D(m,n)=m+n.
(1)请写出两个四位“重九数”: , .
(2)求证:对于任意一个四位“重九数”m,其D(m,n)可被101整除.
(3)对于任意一个四位“重九数”m,记f(m,n)=![]() ,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.
,当f(m,n)是一个完全平方数时,且满足m>n,求满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
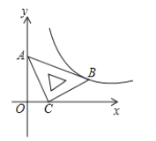
【题目】在平面直角坐标系![]() 中,将-块含有
中,将-块含有![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
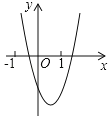
【题目】抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致是( )
在同一坐标系内的图象大致是( )
A.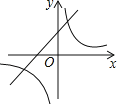 B.
B.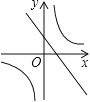
C.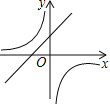 D.
D.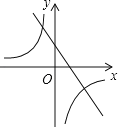
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com