
【题目】如图,某建筑物![]() 上挂着“巴山渝水,魅力重庆”的宣传条幅
上挂着“巴山渝水,魅力重庆”的宣传条幅![]() ,王同学利用测倾器在斜坡的底部
,王同学利用测倾器在斜坡的底部![]() 处测得条幅底部
处测得条幅底部![]() 的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡
的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡![]() 的坡度
的坡度![]() 米,
米,![]() 米(点
米(点![]() 在同平面内,
在同平面内,![]() ,测倾器的高度忽略不计),则条幅
,测倾器的高度忽略不计),则条幅![]() 的长度约为(参考数据:
的长度约为(参考数据:![]()
![]() )
)
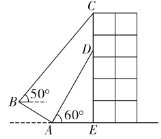
A.12.5米B.12.8米C.13.1米D.13.4米
【答案】B
【解析】
过点B作BF⊥AE于点F,BH⊥DE于点H,在Rt△AFB中,由坡度和勾股定理可以求出BF、AF的长度,在Rt△BHC中,利用三角函数求出CH,再求出DH,最后用CH-DH求出CD即可.
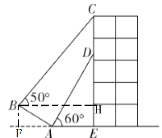
如图所示:
过点B作BF⊥AE于点F,BH⊥DE于点H,
∵![]() 的坡度
的坡度![]() m,
m,
∴![]() ,
,![]() ,
,
∴![]() ,BF为边长,
,BF为边长,
∴解得BF=5,则AF=12m,
∵AE=12m,
∴EF=AF+AE=24(m),
∵∠BHE=∠HEF=∠BFE=90°,
∴四边形BFEH是矩形,
∴EH=BF=5m,BH=EF=24m,
在Rt△BHC中,∠CBH=50°,
∴CH=BH![]()
![]() 24×1.19=28.56(m),
24×1.19=28.56(m),
在Rt△ADE中,∠DAE=60°,
∴DE=AE![]() =12×
=12×![]()
![]() 20.76(m),
20.76(m),
∴CD=CH-DH=28.56-(20.76-5)=12.8(m),
∴条幅CD的长度约为12.8m,
故选:B.


科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在云南大理坐落着美丽的大理三塔.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量三塔中一塔的高度,携带的测量工具有:测角仪.皮尺.小镜子.
(1)小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点![]() ,用测角仪测出看塔顶
,用测角仪测出看塔顶![]() 的仰角
的仰角![]() ,在
,在![]() 点和塔之间选择一点
点和塔之间选择一点![]() ,测出看塔顶
,测出看塔顶![]() 的仰角
的仰角![]() ,然后用皮尺量出
,然后用皮尺量出![]() .
.![]() 两点的距离为
两点的距离为![]() m,自身的高度为
m,自身的高度为![]() m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度(![]() ,结果保留整数).
,结果保留整数).
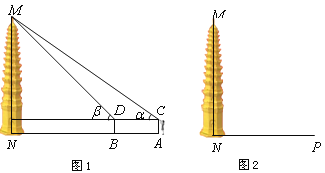
(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影![]() 的长为
的长为![]() m(如图2),你能否利用这一数据设计一个测量方案?如果能,
m(如图2),你能否利用这一数据设计一个测量方案?如果能,
请回答下列问题:
①在你设计的测量方案中,选用的测量工具是: ;
②要计算出塔的高,你还需要测量哪些数据? .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 垂直
垂直![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]()
![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,与边
,与边![]() 相交于点
相交于点![]() ,
,![]() .
.
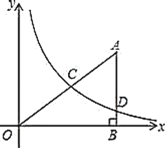
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)经过![]() 、
、![]() 两点的直线的解析式是__________.
两点的直线的解析式是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠EOF=60°,在射线OE上取一点A,使OA=10cm,在射线OF上取一点B,使OB=16cm.以OA、OB为邻边作平行四边形OACB.若点P在射线OF上,点Q在线段CA上,且CQ:OP=1:2.设CQ=a(a>0).

(1)连接PQ,当a=2时,求线段PQ的长度.
(2)若以点P、B、C、Q四点为顶点的四边形是平行四边形时,求a的值.
(3)连接PQ,以PQ所在的直线为对称轴,作点C关于直线PQ的对称点C',当点C′恰好落在平行四边形OACB的边上或者边所在的直线上时,直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
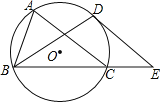
【题目】如图,△ABC为⊙O的内接三角形,∠ABC的角平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证:DE为⊙O的切线;
(2)若DE=![]() AC,求∠ACB的大小.
AC,求∠ACB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A在x轴正半轴上,点B在y轴正半轴上,O为坐标原点,OA=OB=1,过点O作OM1⊥AB于点M1;过点M1作M1A1⊥OA于点A1:过点A1作A1M2⊥AB于点M2;过点M2作M2A2⊥OA于点A2…以此类推,点M2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我县中学生参加“新冠肺炎知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,根据成绩分成如下四个组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,并制作出如下的扇形统计图和直方图.请根据图表信息解答下列问题:
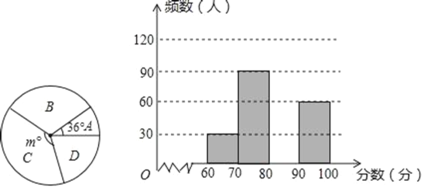
(1)扇形统计图中的m= ,并在图中补全频数分布直方图;
(2)小明的成绩是所有被抽查学生成绩的中位数 ,据此推断他的成绩在 组;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A,C两组学生的概率是多少?请列表或画树状图说明;
(4)若我县学生人数为18000人,请根据上述调查结果,估计我县学生成绩在C、D两组的共多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com