
【题目】如图,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数![]() (
(![]() )与
)与![]() (
(![]() )的图象上,则tan∠BAO的值为( )
)的图象上,则tan∠BAO的值为( )

A.1B.2C.3D.![]()
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
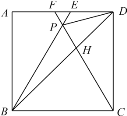
①△ABE≌△DCF;②∠PDF=15°;③![]() ;④
;④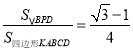 ,其中正确的结论有( )
,其中正确的结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物![]() 上挂着“巴山渝水,魅力重庆”的宣传条幅
上挂着“巴山渝水,魅力重庆”的宣传条幅![]() ,王同学利用测倾器在斜坡的底部
,王同学利用测倾器在斜坡的底部![]() 处测得条幅底部
处测得条幅底部![]() 的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡
的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡![]() 的坡度
的坡度![]() 米,
米,![]() 米(点
米(点![]() 在同平面内,
在同平面内,![]() ,测倾器的高度忽略不计),则条幅
,测倾器的高度忽略不计),则条幅![]() 的长度约为(参考数据:
的长度约为(参考数据:![]()
![]() )
)
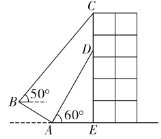
A.12.5米B.12.8米C.13.1米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是( )
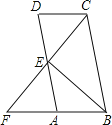
A. FA:FB=1:2 B. AE:BC=1:2
C. BE:CF=1:2 D. S△ABE:S△FBC=1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的边
的边![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,反比例函数
,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() .
.
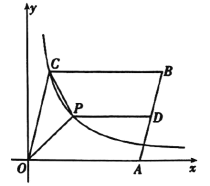
(1)求反比例函数的关系式和点![]() 的坐标,
的坐标,
(2)过![]() 的中点
的中点![]() 作
作![]() 轴交反比例函数图象于点
轴交反比例函数图象于点![]() ,连接
,连接![]() .求△
.求△![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,圆内接四边形ABCD,AD=BC,AB是⊙O的直径.
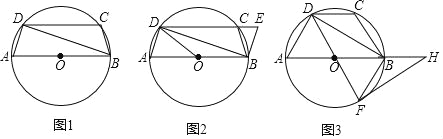
(1)求证:AB∥CD;
(2)如图2,连接OD,作∠CBE=2∠ABD,BE交DC的延长线于点E,若AB=6,AD=2,求CE的长;
(3)如图3,延长OB使得BH=OB,DF是⊙O的直径,连接FH,若BD=FH,求证:FH是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
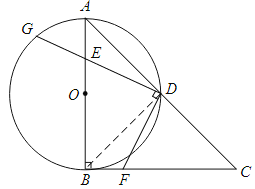
【题目】如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接EF,求证:∠FEB=∠GDA;
(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:在教学课上,老师提出如下问题:尺规作图:作一条线段的垂直平分线.
已知:线段AB.
![]()
求作:线段AB的垂直平分线.
小芸的作法如下:如图, (1)分别以点A和点B为圆心,大于![]() 的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
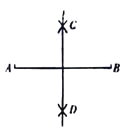
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是____________________,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com